Matematici dal 1800 al 1850

Torna a lista dei Periodi della Matematica.

 1800 – 1850

 

1841 – William Rutherford (1798-1871) calcola 208 cifre di π, di cui 152 sono corrette,  superando il record precedente di Jurij Vega, che nel 1759 diede 126 cifre corrette. Usa:

π /4 = 4arctang (1/5) – arctang (1/70)+ arctang (1/99), derivata dalla formula di MACHIN.

1844 – Zacharias Dase (1824 –  1861) calcola 200 cifre di π.

π /4 = arctang (1/2)+ arctang (1/5)+ arctang (1/8)

1847 – Thomas Clausen, 248 cifre di π.

 

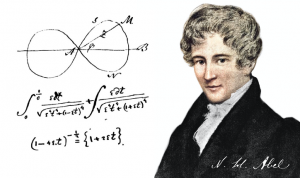Niels Henrik ABEL (1802-1829)- 27, matematico norvegese auto-didatta detto “Il Mozart della matematica“. A 21 anni, forni’  la prima dimostrazione completa del fatto che “non esiste una soluzione per radicali, in funzione dei coefficienti, di un’equazione algebrica generale di grado maggiore di quattro“, risultato oggi noto come Teorema di Ruffini-Abel. Il problema era irrisolto da oltre 250 anni. Abel ha inoltre gettato le basi,  indipendentemente da Galois, per la teoria dei gruppi . A 22 anni scrisse anche un lavoro  sugli integrali ellittici gettando le basi  la teoria delle funzioni ellittiche . Nel 1829, a 26 anni, Abel morì di tubercolosi, contraendo la malattia in un viaggio in slitta nel sud della Norvegia, a dicembre, per visitare la sua fidanzata.(vai a:  )

Giuseppe ALBEGGIANNI (1818-1882). Laureato in ingegneria (1842), fu ordinario di “Introduzione al calcolo” a partire dal 1860 presso l’Università di Palermo. Divenuto preside della Facoltà di scienze matematiche, fisiche e naturali, nel 1869 succede al chimico  Stanislao Cannizzaro nell’incarico di rettore dell’università di Palermo, ruolo che ricoprirà sino al 1874. È stato presidente del Circolo Matematico di Palermo.

 

Cesare ARZELA’ (1847-1912). Si formò alla Scuola Normale Superiore di Pisa, dove si laureò nel 1869, e successivamente insegnò presso le Università di Palermo (cattedra di algebra) nel 1878 e di Bologna (cattedra di calcolo) dal 1880 fino alla sua morte. (per saperne di più).  Il Teorema di Ascoli-Arzelà da una condizione sufficiente a ché una successione di funzioni continue e limitate ammetta una sottosuccessione convergente, nella norma del massimo.  Si tratta della norma che rende  lo spazio delle funzioni continue su un intervallo, uno spazio completo, ovvero uno spazio di Banach.

 

Giulio ASCOLI (1843-1896). Si laureò nel 1868 alla Scuola Normale di Pisa. Dal 1872 insegnò Algebra e Calcolo nel biennio preparatorio del Regio Istituto Tecnico Superiore (futuro Politecnico di Milano). Insegnò pure nell’Istituto Tecnico “Cattaneo” dove una lapide del 1901, lo ricorda. Tra i suoi principali contributi ricordiamo: la teoria delle funzioni di variabile reale e la nozione di successione di funzioni continue “in ugual grado” con il connesso teorema di Ascoli-Arzelà, che indica la possibilità di estrarre da una successione di funzioni, ugualmente continue ed uniformemente limitate, una successione parziale uniformemente convergente. Per il Teorema di Ascoli-Arzelà cfr. Arzelà 1847-1912. Fu socio corrispondente dell’Istituto Lombardo.

 

Albert Victor BACKLUND (1845-1922)

Walter William Rouse BALL (1850-1925) matematico e avvocato britannico. E’ noto soprattutto per le sue opere sulla storia della matematica e sulla matematica ricreativa. Fu membro del Trinity College Cambridge dal 1878 al 1905. Scrisse A Short Account of the History of Mathematics, testo integrale online (prima ed. 1888), Mathematical Recreations and Essays (prima ed. 1892; successive con H.S.M. Coxeter), A History of the First Trinity Boat Club (1908).

Giuseppe BATTAGLINI (1826-1894) matematico napoletano, studiò con Nicolò Fergola (1753-1824), e Enrico D’Ovidio (1843-1933) . Sviluppò la geometria non euclidea in relazione a matematici italiani e stranieri, anche se la sua attività  fu osteggiata dalle scuole  più tradizionaliste, che facevano capo a Vincenzo Flauti (1782-1863)e avversato anche dai suoi allievi che gli impedirono l’accesso all’Università. Nel 1860 fu nominato professore di Geometria superiore da Garibaldi e Flauti perse del tutto la sua importanza.  Nel 1863 fondò con Nicola Trudi (1811-1884) e Vincenzo Janni (1819-1891) il Giornale di matematiche (detto di Battaglini dopo la sua morte). Dopo tre anni rimase solo alla guida e la rivista ebbe un ruolo molto importante e la rivista durò ancora per circa altri 100 anni.. Tra i suoi allievi Enrico D’Ovidio (1843-1933) e i più giovani Alfredo Capelli (1855-1910), Ettore Caporali (1855-1886), Riccardo De Paolis (1854-1892),  Giovanni Frattini (1852-1925) e Domenico Montesano(1863-1886), tutti algebristi italiani del periodo.

N.B. Alla nascita dell’Unità d’Italia si decise di estendere a tutto il territorio nazionale la legge del  Ministro piemontese il Conte Gabrio Casati (1798–1873), datata 13 novembre 1859 n.3725. Fu l’ultima riforma scolastica del vecchio regno. Per le innovazioni  furono nominate apposite commissioni. Nella Commissione per la matematica i maggiori esperti furono il massone bolognese  Luigi Cremona (1830-1903) e il napoletano Giuseppe Battaglini (1826-1894). La commissione decise  che per la geometria si ricorresse, fin dal ginnasio, agli Elementi di Euclide, e successivamente ad una rielaborazione, degli stessi. La successiva legge fu quella del Ministro Michele Coppino (1822-1891), con  la quale escono di scena i testi stranieri, peraltro piuttosto scadenti e nei fatti imposti dal Regno Lombardo Veneto (1815-1866)  e dalla Francia. La Riforma Coppino precedette la Riforma Gentile, costituita da sette Decreti Regi a partire da quello del 31 dicembre 1922, n. 1679 .

Giusto BELLAVITIS (1803-1880). Autodidatta tra il 1822 e il 1843,  pubblicò 25 opere di fisica, chimica e matematica. Nonostante non  fosse laureato, nel 1843 fu nominato professore di matematica al liceo di Vicenza. Ottenne  la laurea ad honorem due anni più tardi, nel 1845, all’Università di Padova, quando già era professore ordinario di geometria descrittiva, geometria analitica e algebra (1845-1880). Nel 1850 divenne socio dell’Accademia nazionale delle scienze. Nel 1866 fu nominato senatore del Regno. Criticò le geometrie non euclidee e in particolare le opere di Lobacevskj.

Eugenio BELTRAMI (1835-1890), fu un matematico e un accademico italiano, noto soprattutto per i suoi contributi alla geometria non euclidea e all’elettroma-gnetismo. Studia a Pavia dal 1853 al 1856 sotto Francesco Brioschi (1824-1897)  ma non riesce però a concludere gli studi per ristrettezze finanziarie. A Milano frequenta l’Osservatorio astronomico di Brera e, su suggerimento di Brioschi, riprende a lavorare su argomenti matematici. Nel 1861 con la costituzione del Regno d’Italia, le cose cambiano, Beltrami pubblica nel 1862 il suo primo articolo e Brioschi riesce a farlo nominare, senza concorso, professore straordinario di algebra e geometria analitica dell’Università di Bologna. Nel 1864 ottiene la cattedra di geodesia all’Università di Pisa, dove entra in amicizia con Enrico Betti e conosce Bernhard Riemann . Nel 1866 ritorna a Bologna per ricoprire la cattedra di meccanica razionale. Nel 1873 viene chiamato alla cattedra di meccanica razionale dell’Università di Roma. Dal 1876 si trasferisce a Pavia per occupare la cattedra di fisica matematica e nel 1891 ritorna a Roma.  Beltrami fu anche importante nell’organizzazione della matematica italiana: presidente dell’Accademia dei Lincei nel 1898, succedendo a Brioschi, fece parte anche dell’Academia delle Scienze di Bologna. Si  occupò di geometria differenziale, riprendendo le opere di Gauss, Riemann, Lobachevsky,  e Luigi Cremona. Studiando le superfici a curvatura negativa ottenne nel 1868 il suo risultato più famoso: nell’articolo Saggio sopra un’interpretazione della geometria non euclidea fornì una concreta realizzazione della geometria non euclidea di Lobachevsky e János Bolyai e la collegò alla geometria di Riemann: si servì di una pseudosfera, superficie generata per rivoluzione di una trattrice intorno al suo asintoto. In questo articolo Beltrami non segnalò esplicitamente di aver provato la consistenza della geometria non euclidea, cioè l’indipendenza del postulato delle rette parallele dagli altri assiomi della geometria euclidea, ma piuttosto sottolineò che János Bolyai e Lobachevsky avevano sviluppato la teoria delle geodetiche sulle superfici di curvatura negativa. La sua prova della indipendenza del postulato delle rette parallele fu sottolineata da Guillaume Jules Hoüel nella sua traduzione in francese dei lavori di Lobachevsky e di Beltrami. Le ricerche di Beltrami sulla teoria dell’elasticità in spazi non euclidei si inserivano nella corrente filosofica naturale, che si sforzava di fornire una spiegazione del mondo in termini meccanici. Beltrami si è occupato anche di ottica, termodinamica, elasticità, teoria del potenziale ed elettromagnetismo. In questo ambito di studi esaminò come avrebbero dovuto esser modificate alcune leggi fisiche per operare in uno spazio a curvatura negativa e diede una generalizzazione dell’operatore di Laplace. Le tecniche differenziali di Beltrami per lo studio dei problemi fisico-matematici influenzarono indirettamente la nascita del calcolo tensoriale fornendo una base per le idee che svilupperanno successivamente Gregorio Ricci-Curbastro e Tullio Levi-Civita. Nel 1899 fu nominato senatore del Regno. Al suo nome è dedicato un asteroide della fascia principale, 15620 Beltrami.

Enrico BETTI (1823-1892). Presso l’Università di Pisa fu allievo per la matematica di Ottaviano Fabrizio Mossotti (1791-1863) e per la fisica di Carlo Matteucci. Nel 1846 si laureò in matematiche applicate, sotto la direzione scientifica di Giuseppe Doveri (1792-1857). Fu professore nei licei di Pistoia e Firenze tra il 1849 e il 1854.  Nel 1857 fu assunto come professore di algebra all’Università di Pisa e poi di Geometria. Collaborò con Francesco Brioschi e Felice Casorati, per visitare i principali centri matematici d’Europa  dove incontrò e diventò amico di Riemann. Fu  direttore della Scuola Normale Superiore di Pisa, dal 1865 al 1874 e dal 1876 al 1892 .Fu più volte deputato al Parlamento , fu segretario generale del ministero della Pubblica istruzione dal 1874 al 1876 e Senatore dei Regno dal 1884. opere didattiche.

 

George BOOLE (1815-1864) (vai a) padre di Alicia BOOLE STOTT (1860-1940)

 

 

Janos BOLAY(1802-1860) matematico ungherese, figlio del matematico Farkas (1775-1856).Deluso per essere stato anticipato da Gauss e Lobacewskj nella scoperta delle geometrie non euclidee cadde in una profonda depressione.  Sembra che in una biblioteca di Cluj-Napoca (oggi in Romania) ci siano suoi manoscritti mai esaminati.

Ludwig  BOLZMANN (1844-1906)

Baldassarre BONCOMPAGNI Ludovisi, principe di Piombino (1821-1894) è stato un matematico e storico della scienza italiano.  Fu editore del celebre Bullettino di Bibliografia  e di storia delle Scienze Matematiche e Fisiche, (1868-1887), il primo periodico italiano interamente dedicato alla storia della matematica. Curò la prima edizione moderna delle opere di Leonardo Fibonacci: il Liber abbaci, la Practica Geometriae, il Liber quadratorum, il Flos e l’Epistola ad magistrum Theodorum. Era in corrispndenza con Catalan.

Francesco BRIOSCI (1824-1897) (vai a profilo)  Matematico e Idraulico.  Ricoprì nel corso della sua vita le cariche di rettore di Pavia e segretario generale del Ministero della Pubblica Istruzione, col Ministro Carlo Matteucci, celebre fisico; fu presidente del Consiglio direttivo dell’Accademia Scientifico-Letteraria, nucleo originario della futura Università degli Studi, e fondatore e direttore dell’Istituto Tecnico Superiore (che poi sarà ribattezzato Politecnico di Milano), il secondo Politecnico d’Italia. Nel 1865 fu nominato senatore dell’IX legislatura del Regno d’Italia. Fu Presidente dell’Accademia dei Lincei.(vai a commemorazione in pdf) – (vai a opere didattiche).  Tra i suoi allievi figurano Eugenio Beltrami, Giuseppe Colombo e Luigi Cremona.

Giuseppe BRUNO (1828-1893). Insegnò nel Collegio Carlo Alberto (1846/1847) poi a Ceva dove insegnò filosofia, poi ritornò a Torino. A Torino insegnò matematica al Collegio Nazionale dal 1850 in poi. Nel 1850 Bruno si laureò in ingegneria idraulica. Dal 1852 al 1858 insegnò algebra e geome-tria  mentre dal 1860 al 1862 insegnò calcolo differenziale e integrale. Nel 1863 insegnò geometria descrittiva all’università. Insegnò geometria proiettiva a partire dal 1875 e nel 1881 divenne il preside della Facoltà di Scienze. Socio dell’Accademia delle Scienze di Torino, fu uno dei maestri di Corrado Segre, che divenne il caposcuola della geometria algebrica italiana. Fu Giuseppe Bruno ad instillare in Segre un grande amore per la geometria, e a convincerlo a dedicarsi alla matematica, anziché all’ingegneria. Segre, che fu poi assistente di Bruno negli anni ottanta, nella nota biografica in sua commemorazione si dichiarò suo discepolo: «A lui che, prima che collega, mi fu maestro, e non solo in matematica ma eziandio nel nobile culto del dovere, l’estremo saluto, reverente e commosso, del suo discepolo!» Bruno fu autore di 21 lavori scientifici, dei quali due di Analisi, su equazioni differenziali lineari e frazioni continue, e i rimanenti di Geometria. Questi ultimi riguardano le coniche, le quadriche e altre superfici. 

Francesco CALDARERA (1825-1920) professore di Meccanica Razionale a Palermo.

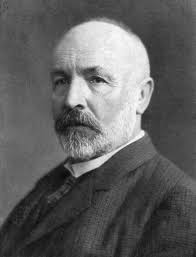George CANTOR (1845 -1918) (scheda).

 

 

Moritz CANTOR (1829-1920) matematico tedesco che insegnò ad Heidelberg, ha scritto tra il 1884 e il 1908 l’opera in 4 volumi  Vorlesungen uber Geschichte der Mathematik (Lezioni di storia della Matematica), dove avanza l’ipotesi che gli Egizi conoscessero delle terne pitagoriche.

John CASEY (1820-1891) era un rispettato geometra irlandese. È più famoso per il teorema di Casey su un cerchio tangente ad altri quattro cerchi, un’estensione del teorema di Tolomeo. Tuttavia, ha contribuito con numerose nuove prove e prospettive sulla geometria euclidea.

 

Felice CASORATI (1835-1890)

 

 

 

 

Eugene Ch. CATALAN (1814-1894). Era docente a Liegi e Cesaro fu suo allievo a Liegi e l’aiutò nel corso della sua carriera. Cesaro per l’iltimo anno di studi si trasferì a Roma.

Arthur CAYLEY (1821-1895)

 

 

 

Pafnuti L’vovic CEVYSEV (1821-1894)

Domenico CHELINI (1802-1878) matematico e sacerdote degli Scolopi. Fu espulso per futili motivi.

Rudolph CLEBSCH (1833-1872)

William Kingdom CLIFFORD (1845-1872)

Delfino CODAZZI (1824 – 1873) è stato un matematico, allievo di Antonio Maria Bordoni (1788-1860) noto soprattutto per i suoi risultati nella geometria delle superfici. Dopo la conclusione dei suoi studi, insegnò nelle scuole secondarie, prima a Lodi e poi a Pavia e contemporaneamente si dedicò a ricerche in geometria differenziale. Nel 1859 concorre per un premio bandito dalla Accademia delle scienze francese per una ricerca sulla totalità delle superfici di un dato elemento lineare. Al concorso furono presentati tre lavori di valore da parte di Codazzi, Edmond Bour e Pierre Ossian Bonnet. Nel lavoro di Codazzi venivano date le condizioni necessarie e sufficienti per la possibilità di porre in corrispondenza due superfici e comparivano le formule ora note come formule di Mainardi-Codazzi. Queste formule erano state già trovate da Gaspare Mainardi e pubblicate nel 1856 e nel 1853 erano comparse in una dissertazione di Karl M. Peterson, studente di Ernst Ferdinand Adolf Minding. Tuttavia Codazzi le aveva ottenuta con una dimostrazione indipendente e con una formulazione più semplice.Il lavoro presentato da Codazzi, che non era stato pubblicato su riviste autorevoli come quelli di Bour e Bonnet, ottenne solo una menzione onorevole ma gli diede notorietà e gli fece ottenere una cattedra di “Algebra e Geometria analitica” all’Università di Pavia nel 1865. Successivamente si dedicò a ricerche sulle coordinate curvilinee che portarono ad un lavoro dal titolo Sulle coordinate curvilinee d’una superficie e dello spazio pubblicato in 5 parti dal 1867 al 1871. All’Università di Pavia rimase fino alla fine della sua non lunga vita. Egli ottenne anche risultati sulle linee isometriche, sui triangoli geodesici e sulla stabilità dei corpi fluttuanti.

Paul J. COHEN (1934-2007) – 73. Ha operato nel MIT e a Princeton. Medaglia Fields nel 1966, ricevuta per aver trovato nel  1963 uno dei più spettacolari risultati della matematica contemporanea, ovvero la prova dell’indipendenza dell’ipotesi del continuo dagli assiomi della teoria degli insiemi di Zermelo-Fraenkel. 

Luigi CREMONA (1830-1903) – 73. (vai a)

 

 

 

Alexander  CRUM BROWN (1838-1922) grafi

Gaston DARBOUX (1842-1917)

 

 

 

Julius William DEEDEKIND (1831-1916) -87. Fu allievo di Moritz Abraham Stern (1807-1894), studioso di teoria dei numeri. Dedekind consegue il dottorato nel 1852 sotto la supervisione di Gauss (sarà il suo ultimo allievo) presentando una dissertazione sulla teoria degli integrali di Eulero.  Il suo maggior contributo è la costruzione del campo dei numeri reali mediante il metodo dei cosiddetti tagli di Deedekind, del tutto equivalente alla definizione mediante classi contigue.  Dimostrò il postulato di continuità che porta il suo nome equivalente ai due assiomi di Cantor (1845 -1918) e di Archimede.

Giovanni DE BERARDINIS (1846-1937) di Teramo, professore di Geodesia a Napoli.

Tommaso DEL BECCARO  Milano

Augustus DE MORGAN (1806-1871) (vai a). 

 

 

Nicola Salvatore DINO (1843-1919) – 76. vedi SALVATORE- DINO.

Professore di Geometria e deputato.

 

 

Charles DODSON (1832-1898) alias Lewis Carrol , logico e matematico inglese, famoso per Alice nel Paese delle meraviglie. Ha scritto Euclid and his modern rivals, Il gioco della logica, Una storia ingarbugliata.

Enrico  D’OVIDIO (1843-1933) -90. Matematico molisano operante a Torino, fu allievo del Battaglini (1826-1894).

Enrico (1843-1933) -90 era nipote di Achille Sannia, ma anche suo cognato avendo Achille Sannia sposato la sorella  Angela D’Ovidio.

 

Ulisse DINI (1845-1918) – professore di Analisi Matematica a Pisa – Teorema del Dini

 

 

 

Arthur Stanley EDDINGTON (1882-1944). Astrofisico. Eddington amava, oltre alla scienza, la filosofia e la teologia, come tutti i giganti di Cambridge : Isaac Newton, Michael Faraday e James Maxwell. La sua fede cristiana è  espressa in, La scienza & il mondo invisibile. Scoprì il limite che porta il suo nome (limite di Eddington): corrisponde alla luminosità massima che può avere una stella con una data massa, senza che essa inizi a perdere gli strati più alti della propria atmosfera. Fu grazie a uno dei suoi articoli (Report on the relativity theory of gravitation), che gli anglosassoni scoprirono la teoria della relatività generale di Albert Einstein. 

Francesco FAA’ di BRUNO (1825-1888)  è stato un ufficiale, matematico e presbitero italiano. Dopo aver militato nell’esercito sabaudo, divenne professore di matematica presso l’università e l’accademia militare di Torino. Pubblicò importanti studi sulle teorie della eliminazione e degli invarianti e sulle funzioni ellittiche. In seguito venne ordinato sacerdote e fondò l’Opera di Santa Zita, la congregazione delle Suore Minime di Nostra Signora del Suffragio e un istituto scolastico a Torino, che oggi comprende scuola materna, elementare e media. È stato beatificato da papa Giovanni Paolo II il 25 settembre 1988. È considerato, ancorché non canonizzato, uno dei santi sociali torinesi.

 

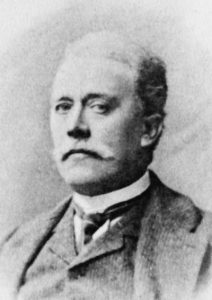
Aureliano FAIFOFER (1843-1909) (vai a)

 

 

 

 

Gottlob FREGE (1848-1925)

Ferdinand George FROBENIUS (1849-1917) è stato un matematico tedesco, noto soprattutto per i suoi contributi alla teoria delle equazioni differenziali e alla teoria dei gruppi. Frobenius nel 1878 ha  dimostrato che qualunque corpo (anche non commutativo) che contenga il campo dei numeri reali come sottocorpo e tale che ogni suo elemento soddisfi un’equazione polinomiale a coefficienti reali deve essere isomorfo ai numeri reali, oppure ai numeri complessi. oppure ai quaternioni.

 

Evaristide GALOIS (1811-1832) (minischeda)

 

 

Giovanni GARBIERI (1847-1931)  opere didattiche

Angelo GENOCCHI (1817-1889) predecessore di PEANO allievo di PLANA (1781-1864). Nel 1838 si laureò in giurisprudenza a Parma ,esercitò la professione forense, nel 1846 ebbe  la cattedra di Diritto romano,  tuttavia non era né un bravo avvocato, né un bravo insegnante. I suoi interessi in  politica erano  le idee liberali e antiaustriache, dopo la Prima guerra d’indipendenza italiana del 1848 si trasferì a Torino, dove seguì le lezioni di matematica di Giovanni Plana (1781-1864). Nel 1859 ottenne la cattedra di Algebra e Geometria complementare, che nel 1862 lasciò per quella di Calcolo infinitesimale. Giuseppe  Peano (1858-1932), che gli succedette nella cattedra, fu suo assistente nel 1881-82. Fu socio dell’Accademia delle Scienze di Torino, presiedendola dal 1885 alla sua morte, e Senatore del Regno d’Italia dal 1886. Nelle sue ricerche privilegiò la teoria dei numeri, al tempo piuttosto negletta, la teoria delle serie, e gli integrali euleriani, usando sempre un approccio critico e attento ai fondamenti della matematica. I numeri di Genocchi, G₁, G₁, G₂, … sono i termini dello sviluppo in serie seguente:

I primi valori  sono: 1, -1, 0, 1, 0, -3, 0, 17, 0, -155, 0, 2073, 0, -38227, 0, 929569, si noti che quelli d’ indice dispari > 1 sono nulli. Nel 2004 D. Terr ha dimostrato che i soli numeri di Genocchi che sono primi sono G₆ = -3 e G₈ = 17.

Gilberto GOVI (1826-1888) – 62

Hermann Günther GRASSMANN (1809-1877)

Francis  GUTHRIE (1831-1899) Grafi

Carl Gustav JACOBI (1804-1851)

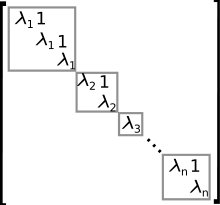M.E. Camille  JORDAN (1838-1922). Lavorò in algebra e Teoria dei gruppi applicandola anche ai cristalli. Completò e divulgò l’opera di Galois. Introdusse l’omitipia come eguaglianza di colori e forma. Teorema di Jordan. Ogni curva semplice e chiusa divide il piano in due parti tali che tra due punti di una medesima parte si può tracciare una poligonale che non incontra la curva , cosa che non accade per due punti da parte diversa. 

 

Vincenzo JANNI (1819-1891).  Giuseppe Battaglini, Nicola Trudi e Vincenzo Janni fondarono il Giornale di Matematica (detto poi di Battaglini) nel 1863, ma dopo tre anni lasciarono da solo Battaglini, la rivista durò ancora per circa altri 100 anni.

Georges Henri HALPHEN (1844-1889)

William Rowan  Hamilton (1805-1865) grafi e inventore dei quaternioni

Helmut HASSE (1898 – 1979)

Edward HEINE (1821-1881)

Charles HERMITE (1822-1901)

Gerhald HESSEMBERG (1874-1925)

Carl Fridolin Bernardh HIERHOLZER (1840-1871) – 31  grafi

Ludwig Otto HOLDER (1859- 1937)

Joules HUEL (1825-1866) 

Adolf HURWITZ (1859-1919)

 

 

 

Karl Joseph KAPPER (1828-1899)

Alfred Bray  KEMPE (1849-1922) grafi

Wilheim KILLING (1847-1923)

Gustave Robert KIRCHOFF (1824-1887)

Thomas Penyngton KIRKMAN (1806-1895)

Felix Christian KLEIN (1849-1925)  (vai a)

 

 

Leo KONISBERG (1837-1921)

Leopold KRONECKER (1823-1891)

Sof’ia Vasil’evna KOVALEVKAYA (1850-1891) (minischeda)

Edmond Nicolas LAGUERRE (1834-1886)

Pierre Alphonse LAURENT (1813-1854)

Marius Sophus LIE (1842-1899)

Rudolph LIPSCHITZ (1832-1903) 

Johann Benedict LISTING (1808-1882) matematico e fisico

Ada Lovelace (1815-1852) è stata una matematica e scrittrice inglese. È considerata la prima programmatrice di computer. Lovelace ha lavorato con Charles Babbage allo sviluppo della macchina analitica, il primo computer programmabile. Ha anche scritto il primo programma per la macchina analitica, che è considerato il primo programma per computer della storia.

François Édouard Anatole LUCAS  (1842 – 1891) è stato un matematico francese. È noto per i suoi studi sulla teoria dei numeri, in particolare sulla successione di Fibonacci, e sul test di primalità per i numeri di Mersenne oggi detto test di Lucas-Lehmer. La successione di Lucas, legata a quella di Fibonacci, porta il suo nome. Nel 1857 (aveva 15 anni) si occupò della primalità del numero 2¹²⁷-1 e solo nel 1876 provò che era  primo. Tale numero rimase il più grande numero primo di Mersenne conosciuto per tre quarti di secolo, e probabilmente resterà per sempre il più grande trovato senza l’aiuto del computer.

Filippo MAGGIACOMO (   -1895)

Gaspare MAINARDI (1800-1879) vedi Codazzi. Si laureò a Pavia dove fu assistente e supplente a partire dal 1822. Nel 1840, fu nominato ordinario d’introduzione al calcolo e poi di calcolo infinitesimale, insegnamento che lasciò nel 1863 divenendo professore emerito. Autore di una sessantina di lavori di analisi e teoria delle superfici, oggi è soprattutto ricordato per le formule di Codazzi-Mainardi (semplificate da Codazzi), fondamentali in geometria differenziale (i 6 coefficienti delle due forme differenziali fondamentali di una superficie sono legati da tre equazioni differenziali, di cui una fu stabilita da Gauss e le altre due da Mainardi).  Fu socio dell’Accademia dei Lincei e dell’Istituto Lombardo. Necrologio: Rend. Ist. Lombardo, (2), 12, (1879) (Belgioioso).

Paul MANSION (1844-1919) Allievo di Catalan , docente a Gand. Fu editore con Neuberg ((1840-1926) della rivista “MATHESIS” che sostituì Nouvelle Correspondance Mathematique.

Carlo MATTEUCCI (1811-1868)

Emile Leonards MATHIEU (1835-1890)

 

James Clerk MAXWELL (1831-1879)

 

 

 

Luigi Federico MENABREA  (1809-1896) dei  marchese di Valdora, è stato un nobile, ingegnere, generale, politico e diplomatico italiano.  Fu tra gli allievi prediletti di G. Plana e G. Bidone, conseguì dapprima la laurea in ingegneria idraulica, nel 1832, poi quella in architettura civile nel1833 . Ottenuta la libera docenza in matematica nel 1835, a Torino fu insegnante di meccanica applicata, balistica, geometria e geodesia nella scuola d’applicazione e di geometria descrittiva all’Accademia militare. I successi in campo scientifico giunsero all’inizio del 1839, per la  memoria relativa al calcolo della densità della Terra (Calcul de la densité de la Terre: suivi d’un mémoire sur un cas spécial du mouvement d’un pendule, Turin 1839), fu socio dell’Accademia delle Scienze di Torino e dell’Accademia Nazionale dei Lincei.Come politico dall’ottobre 1866 al 1869 fu Presidente del Consiglio dei Ministri.

 

Charles MERAY (1835-1911)

 

famoso per il sistema introduttivo dei numeri reali (metodo di Meray-Cantor).

 

Gosta MITTAG LEFFLER (1846-1927), noto in quanto fu la causa della esclusione dei matematici dal premio Nobel, per via dei  contrasti tra lo stesso Nobel Mittag Leffler  a causa di questioni di donne, delle cui emancipazioni Mittag Leffler, era un appassionato difensore e promotore! 

 

Joseph Jean-Baptiste NEUBERG  (1840-1926). Allievo di Catalan , docente a Liegi, ebbe Cesaro per allievo. Fu editore con Mansion (1844-1919)  della rivista MATHESIS” che sostituì Nouvelle Correspondance Mathematique, riviste sulle quali pubblicò molti lavori E. Cesaro..

Max NOETHER (1844-1921)

Fortunato PADULA (1815-1881), Meccanica razionale a Napoli.

Théophile PEPIN (1826 – 1904), matematico gesuita. Si occupò  di teoria dei numeri. Nel 1876 diede una dimostrazione dell’ultimo teorema di Fermat per n = 7. Il Test di Pépin è usato per vedere se un numero di Fermat è primo. Nel 1863 pubblicò una memoria negli Annali di Mate-matica sul problema di Liouville di trovare integrali razionali di equazioni differenziali lineari con coefficienti razionali. Liouville considerò l’equazione nella forma d² y / d x² = P y. Pépin ne diede una soluzione rimuovendo le restrizioni su y. Pubblicò alcune opere sui lavori postumi di Gauss sulle funzioni ellittiche. Nel 1880 fu il primo a dare una soluzione al sistema di equazioni diofantee x² + y² = z², x² = u² + v², x – y = u – v proposto da Frénicle de Bessy (1605-1675).

Julius Peter Christian  PETERSEN (1839-1910) grafi

Giacomo PLATNER (1833-1897) prof. di Algebra complementare. Collaborò al libro “Gli elementi di Euclide …” di Enrico Betti e Francesco Brioschi al quale mise mano anche Luigi Cremona per la prefazione e alcuni capitoli. Platner fece diverse traduzioni da libri stranieri e fece tutte le figure.

Julius PLUCKER (1801-1868)

Giuseppe PONCINI (1814-1850) – 36. Srisse “Le equazioni numeriche, intiere e razionali ad una incognita“. 

Michel REISS (1805-1869)

Carl Theodor REYE (1838-1919)

Eugene ROUCHE’ (1832-1910) (vai a)

 

 

Raffaele RUBINI (1817-1890)

George SALMON (1819-1904)

Nicola SALVATORE- DINO (1843-1919) – 76.Formatosi a Napoli sotto Achille Sannia (1822-1892), fu professore di Geometria a Roma e dal 1888 a Napoli. Fu deputato.

 

 

Achille SANNIA (1822-1892) nacque a Campobasso, successivamente si trasferì dal Molise a Napoli dove studiò presso lo studio privato di Francesco Paolo Tucci e Salvatore de Angelis, alla Scuola di applicazioni di ponti e strade dove entrò nel 1840, tra i primi al concorso di ammissione. Ne uscì laureato nel 1847 e continuò a perfezionarsi in matematica sotto la guida del professor Carlo D’Andrea. Enrico D’Ovidio (1843-1933) -90 suo allievo era anche suo nipote, ma anche suo cognato avendo Achille Sannia sposato la sorella  Angela D’Ovidio. Nel 1853 fu incaricato presso la Scuola di applicazioni di ponti e strade dell’insegnamento della geometria a tre coordinate e nel 1854 successe a Francesco Paolo Tucci nell’insegnamento della geometria descrittiva. Nel 1856 ottenne il rescritto sovrano che lo autorizzava ad aprire uno studio privato di matematica, com’era allora in uso a Napoli, in via Guantai nuovi prima e a S. Chiara dopo. La scuola acquisì fama sempre maggiore, con circa 200 alunni paganti ai quali Sannia impartiva personalmente lezioni di aritmetica, algebra, trigonometria, algebra complementare, geometria analitica a due e a tre coordinate, calcolo infinitesimale, geometria descrittiva, eccanica razionale. Passò  all’Università nel 1865 come docente di geometria dove ebbe colleghi i più datati  Nicola Fergola (1753),  Felice Giannattasio  (1759),  Annibale Giordano (1769) e Vincenzo Flauti (1782).  Creò nel 1871 una Scuola di elettrotecnica. Lasciò due trattati importanti, uno riguardante la geometria proiettiva e l’altro la geometria elementare. Riorganizzò gli studi matematici dopo la caduta dei Borboni. Ebbe come allievi Salvatore Dino, Giuseppe Battaglini (1826) ed Enrico D’Ovidio. Fu socio dell’Accademia delle Scienze. Fu deputato nella XIII e XVI legislatura e senatore del Regno d’Italia nella XVIII legislatura. Ebbe un figlio, Gustavo Sannia, anch’egli matematico. Grande ufficiale dell’Ordine della Corona d’Italia, Commendatore dell’Ordine dei Santi Maurizio e Lazzaro.

 

Achille SANNIA (1822-1892), matematico molisano, studia a Napoli e ha come allievo principale  Enrico D’Ovidio.

Sarà Deputato nella XIII e XVI legislatura e Senatore nella XVII legislatura. Rordinerà gli studo del Regno delle Due Sicilie.

 

Ernst SCHODER (1841-1902)

 

 

 

Ludvig SCHLAFLI (1814.1895)

C.H.A. SCHWARTZ (1843-1921)

Francesco SIACCI (1839-1907) – 68. Maggiore di artiglieria , fu dal 1892 ordinario di Meccanica Razionale a Napoli. Fu deputato al Parlamentoper due legislature e senatore dal 1902.

Moriz Abraham STERN (1807 – 1894), è stato un matematico tedesco,  successore di Carl Friedrich Gauss nel 1858, e fu il primo professore ordinario di una università tedesca di origine ebrea. Ebbe per allievi Bernhard Riemann e Richard Deedekind e e collaborò con Ferdinand Eisenstein nella formulazione di una dimostrazione del teorema di reciprocità quadratica. Stern si è interessato dei numeri primi che non possono essere espressi come somma di un altro primo e del doppio di un intero quadrato; questi numeri ora sono chiamati primi di Stern. E’ anche noto per aver scoperta la  serie diatomica di Stern che conta il numero dei modi di scrivere un intero naturale come somma di potenze di 2 usando ciascuna potenza non più di una volta. 

Si tratta della successione     1 1, 2, 1, 3, 2, 3, 1, 4, …

James  Joseph SYLVESTER (1814-1897)

Ludwig Peter SYLOW (1832-1918)

Peter Guthrie TAIT (1831-1901) grafi

Jules TANNERY (1848-1910).

Gabriele TORELLI (1849-1931)

Barnaba TORTOLINI (1808-1874) Fondò gli Annali di Scienze matematiche  e fisiche di Tortolini edito a Roma dal 1850 al 1865 dal 1858 si chiama Annali di a pura re applicata. E’ la  prima rivista italiana del settore. Riparte nel 1867 sotto Brioschi e Cremona come annali di Matematica.

Nicola TRUDI (1811-1884) è , principalmente conosciuto per i suoi contributi alla teoria dei determinanti su cui nel 1862 ha pubblicato uno dei primi trattati. Definì i determinanti di Trudi, generalizzazione dei determinanti di Vandermonde. Fu Professore di calcolo infinitesimale presso l’Università di Napoli, e autore di lavori scientifici riguardanti l’analisi nell’ambito della teoria delle funzioni ellittiche. Fu socio del Reale Istituto d’Incoraggiamento di Napoli, del l’Accademia Pontaniana e dell’Accademia delle Scienze fisiche e matematiche di Napoli, della quale fu presidente in tre occasioni: nel 1869, 1877 e 1883.  Abitò a Napoli nel palazzo Filangieri d’Arianello. Tra i suoi allievi vi fu Pasquale Del Pezzo.  Giuseppe Battaglini, Nicola Trudi e Vincenzo Janni fondarono il Giornale di Matematica (detto poi di Battaglini) nel 1863, ma dopo tre anni lasciarono da solo Battaglini, la rivista durò ancora per circa altri 100 anni.

Karl WEISTRASS (1815-1897)

Hieronimis ZEUTHEN (1839-1929) , matematico e storico danese.