torna a lista dei periodi della M.
1500 – 1700
- 1573. Valenthus Otho(1545-1603) calcola le prime 6 cifre di � π.
1585 Del personaggio si trova traccia nel 1585 nei lavori del matematico olandese Adriaen Anthonisz of Adriaen Anthonisz van Alcmaer (1541 – 1620), famoso ingegnere delle fortificazioni, che nel 1585 riscopre che il valore di π può essere approssimato dalla frazione 355/113, che sarebbe il numero di Zu Chongzhi. Adriaan Metius Anthonisz (1571-1635), figlio di Adriaen, geometra olandese, pubblicò il risultato del padre che alcuni chiamano numero di Metius.
- 1593. François Viète(1540-1603) calcola 9 cifre di π.
- � Il fiammingo Adriaan van Roomen (1561 –1615) calcola 16 cifre di π.
- 1596. Ludolph van Ceulen(1540-1610) calcola 20 cifre di � π.
- Ludolph van Ceulen (1540-1610) calcola π con 35 cifre decimali di � πutilizzando poligoni con più di 2 miliardi di lati. Ceulen, fiero di questo risultato, lo farà scrivere sulla sua tomba.
- 1663. Muramatsu Shigekiyo(1608 – 1695) in Giappone trova 7 cifre decimali esatte di π.
1655: John Wallis trova un prodotto infinito razionale per calcolare π.
1655 William Brouncker trova una frazione continua per calcolare π
1665 Isaac Newton calcolò π fino alla sedicesima cifra decimale
1671: James Gregory scopre le serie delle arcotangenti
1674: Leibniz scopre la serie delle arcotangenti per �il calcolo di π.
- π con 4 cifre decimali fu trovato dal matematico e gesuita polacco Adam Adamandy Kochański(1631-1700) un suo trattato del 1685 desunto da una costruzione geometrica.
1699: Abraham Sharp calcola 72 cifre di π.
 Francis BACON (1561-1626). Formatosi con studi in legge e giurisprudenza, divenne un sostenitore e strenuo difensore della Rivoluzione scientifica sostenendo il metodo induttivo fondato sull’esperienza, in senso gnoseologicamente antitetico al metodo deduttivo cartesiano, nonché base della futura teoria della tabula rasa lockiana, espressione che allude alla mancanza di conoscenze a priori e, quindi, già a partire da Aristotele, si esprime l’idea che l’essere umano nasce senza nulla di innato dal punto di vista conoscitivo. In Novum Organum Scientiarum elabora una procedura di lavoro per poter raggiungere una conoscenza certa di un fenomeno. Tale procedura, definita metodo baconiano, consta di due parti fondamentali: la pars destruens e la pars costruens. Nella prima occorre liberare la mente dalle false credenze e convinzioni,
Francis BACON (1561-1626). Formatosi con studi in legge e giurisprudenza, divenne un sostenitore e strenuo difensore della Rivoluzione scientifica sostenendo il metodo induttivo fondato sull’esperienza, in senso gnoseologicamente antitetico al metodo deduttivo cartesiano, nonché base della futura teoria della tabula rasa lockiana, espressione che allude alla mancanza di conoscenze a priori e, quindi, già a partire da Aristotele, si esprime l’idea che l’essere umano nasce senza nulla di innato dal punto di vista conoscitivo. In Novum Organum Scientiarum elabora una procedura di lavoro per poter raggiungere una conoscenza certa di un fenomeno. Tale procedura, definita metodo baconiano, consta di due parti fondamentali: la pars destruens e la pars costruens. Nella prima occorre liberare la mente dalle false credenze e convinzioni,
Claude-Gaspar BACHET de MEZIRAC (1581–1638) è stato un matematico francese, profondo conoscitore di ebraico, greco, latino, italiano e spagnolo. Fu membro dell’Ordine dei Gesuiti per un anno nel 1601. Studiò presso il Collegio gesuita di Reims, dove fu discepolo del matematico Jacques de Billy, (1602 –1679) del quale divenne intimo amico. Passò poi ad insegnare presso il Collegio dei Gesuiti di Milano prima di rinunciare a prendere i voti e dedicarsi allo studio della matematica e alla traduzione di poeti latini e matematici greci.
 Isaac BARROW (1630-1667) è stato un matematico, teologo,. Gli viene attribuito un ruolo non di primo piano, nello sviluppo del moderno calcolo infinitesimale. Isaac Newton fu allievo di Barrow. E’ ricordato per i suoi lavori sul calcolo della tangente: si ritiene sia stato il primo a calcolare le tangenti della curva kappa. .
Isaac BARROW (1630-1667) è stato un matematico, teologo,. Gli viene attribuito un ruolo non di primo piano, nello sviluppo del moderno calcolo infinitesimale. Isaac Newton fu allievo di Barrow. E’ ricordato per i suoi lavori sul calcolo della tangente: si ritiene sia stato il primo a calcolare le tangenti della curva kappa. .
Nel 1669 si dimise dalla sua cattedra per far posto al suo allievo, Isaac Newton.
 George BERKLEY (1685-1735) è stato un filosofo, teologo e vescovo anglicano irlandese, uno dei tre grandi empiristi britannici assieme a John Locke e David Hume. Ignorato e deriso in vita per le sue tesi è oggi ampiamente rivalutato e considerato come una sorta di precursore indiretto di Ernst Mach, Albert Einstein e Niels Bohr per la sua tesi sull’inesistenza della materia e sull’impossibilità di un tempo e uno spazio oggettivamente assoluti. Criticò la dottrina di Isaac Newton di spazio, tempo e movimento assoluti nel De Motu (Sul Moto), pubblicato nel 1721, e nel 1734 pubblicò L’analistaː un discorso indirizzato ad un matematico infedele, una critica dei fondamenti del calcolo, nello sviluppo della matematica.
George BERKLEY (1685-1735) è stato un filosofo, teologo e vescovo anglicano irlandese, uno dei tre grandi empiristi britannici assieme a John Locke e David Hume. Ignorato e deriso in vita per le sue tesi è oggi ampiamente rivalutato e considerato come una sorta di precursore indiretto di Ernst Mach, Albert Einstein e Niels Bohr per la sua tesi sull’inesistenza della materia e sull’impossibilità di un tempo e uno spazio oggettivamente assoluti. Criticò la dottrina di Isaac Newton di spazio, tempo e movimento assoluti nel De Motu (Sul Moto), pubblicato nel 1721, e nel 1734 pubblicò L’analistaː un discorso indirizzato ad un matematico infedele, una critica dei fondamenti del calcolo, nello sviluppo della matematica.
Jakob BERNOULLI (1654-1705) – 51 Albero Famiglia Bernoulli
Johannes I BERNOULLI (1667-1748) – 81, Albero Famiglia Bernoulli
Nicolaus I BERNOULLI (1687- 1759) – 72, figlio di Nicolaus il pittore fratello di Jacob e Johannes I, Albero Famiglia Bernoulli
Nicolaus II BERNOULLI (1695- 1726) – 31 Albero Famiglia Bernoulli
(vai ai Bernoulli del 1700)
Frénicle de BESSY (1605-1675). Propose lo studio del sistema di equazioni diofantee x² + y² = z², x² = u² + v², x – y = u – v, risolto nel 1880 da…..
 Mario BETTINI (1582-1657) matematico ed astronomo gesuita. Gli è stato dedicato da Giovanni Riccioli il cratere Bettinus sulla Luna, situato nella parte sud-occidentale della faccia visibile della Luna.
Mario BETTINI (1582-1657) matematico ed astronomo gesuita. Gli è stato dedicato da Giovanni Riccioli il cratere Bettinus sulla Luna, situato nella parte sud-occidentale della faccia visibile della Luna.
 Jacques de BILLY (1602 –1679), matematico gesuita, maestro e amico di Claude BACHET de Méziriac (1581–1638) e di Jacques Ozanam (16 giugno 1640 –1718) . Billy era in corrispondenza con Pierre de Fermat (1601-1665) e ottenne molti risultati nella teoria dei numeri che portano il suo nome. Bachet introdusse Billy anche all’analisi indeterminata. Opera: Jacques de Billy, Diophantus redivivus, 1-2.
Jacques de BILLY (1602 –1679), matematico gesuita, maestro e amico di Claude BACHET de Méziriac (1581–1638) e di Jacques Ozanam (16 giugno 1640 –1718) . Billy era in corrispondenza con Pierre de Fermat (1601-1665) e ottenne molti risultati nella teoria dei numeri che portano il suo nome. Bachet introdusse Billy anche all’analisi indeterminata. Opera: Jacques de Billy, Diophantus redivivus, 1-2.
Da non confondere con Jacques de BILLY de Prunay (Jacobus Billius) (1535-1581), abate benedettino che fu un importante umanista, traduttore di opere dei Padri della Chiesa greca.
 Raffaele BOMBELLI (1526-1572) è stato un matematico e ingegnere italiano. Gli unici due cenni di cui disponiamo su Bombelli sono quelli che egli stesso fornisce nella prefazione alla sua opera fondamentale, L’algebra, parte maggiore dell’aritmetica (1572). Tradusse gran parte dell’opera di Diofanto. La sua opera doveva essere in cinque volumi: i primi tre furono pubblicati nel 1572 (con il titolo completo di L’Algebra, opera di Rafael Bombelli da Bologna, divisa in tre libri con la quale ciascuno da sé potrà venire in perfetta cognitione della teoria dell’Aritmetica), mentre il quarto e il quinto, sulla geometria, restarono manoscritti, a causa della morte prematura di Bombelli. I manoscritti, riscoperti nel 1923, furono stampati solo nel 1929.
Raffaele BOMBELLI (1526-1572) è stato un matematico e ingegnere italiano. Gli unici due cenni di cui disponiamo su Bombelli sono quelli che egli stesso fornisce nella prefazione alla sua opera fondamentale, L’algebra, parte maggiore dell’aritmetica (1572). Tradusse gran parte dell’opera di Diofanto. La sua opera doveva essere in cinque volumi: i primi tre furono pubblicati nel 1572 (con il titolo completo di L’Algebra, opera di Rafael Bombelli da Bologna, divisa in tre libri con la quale ciascuno da sé potrà venire in perfetta cognitione della teoria dell’Aritmetica), mentre il quarto e il quinto, sulla geometria, restarono manoscritti, a causa della morte prematura di Bombelli. I manoscritti, riscoperti nel 1923, furono stampati solo nel 1929.
 Henry BRIGGS (1561-1630) introdusse i logaritmi in base 10 e pubblicò le sue tavole dei logaritmi.
Henry BRIGGS (1561-1630) introdusse i logaritmi in base 10 e pubblicò le sue tavole dei logaritmi.
 Gerolamo CARDANO (1501-1576) (vai al pdf)
Gerolamo CARDANO (1501-1576) (vai al pdf)
 Padre Sertorio CAPUTO (1556-1608), (vai a) fondatore dell’Accademia dei Velati ( F.Eugeni – D.Marconi – Storia_dell ‘Accademia Piceno Aprutina dei Velati – APAV).
Padre Sertorio CAPUTO (1556-1608), (vai a) fondatore dell’Accademia dei Velati ( F.Eugeni – D.Marconi – Storia_dell ‘Accademia Piceno Aprutina dei Velati – APAV).
 Renato CARTESIO (1596-1650) Renè Descartes estese la concezione razionalistica di una conoscenza ispirata alla precisione e certezza delle scienze matematiche a ogni aspetto del sapere, dando vita a quello che oggi è conosciuto con il nome di razionalismo continentale, una posizione filosofica dominante in Europa tra il XVII e il XVIII secolo. (minischeda)
Renato CARTESIO (1596-1650) Renè Descartes estese la concezione razionalistica di una conoscenza ispirata alla precisione e certezza delle scienze matematiche a ogni aspetto del sapere, dando vita a quello che oggi è conosciuto con il nome di razionalismo continentale, una posizione filosofica dominante in Europa tra il XVII e il XVIII secolo. (minischeda)
 Giovanni Domenico CASSINI (1625 – 1712) è stato un matematico, astronomo, ingegnere, medico e biologo italiano naturalizzato francese. Prima della naturalizzazione francese, avvenuta nel 1673, Cassini lavorò a fasi alterne come astronomo presso l’Osservatorio di Panzano di Castelfranco Emilia, dal 1648 al 1664; cioè fino alla morte del marchese Cornelio Malvasia, suo mecenate e signore del Castello di Panzano il avvenuta in quell’anno. Fu professore di astronomia all’Università di Bologna e nel 1671 divenne il direttore dell’Osservatorio di Parigi.
Giovanni Domenico CASSINI (1625 – 1712) è stato un matematico, astronomo, ingegnere, medico e biologo italiano naturalizzato francese. Prima della naturalizzazione francese, avvenuta nel 1673, Cassini lavorò a fasi alterne come astronomo presso l’Osservatorio di Panzano di Castelfranco Emilia, dal 1648 al 1664; cioè fino alla morte del marchese Cornelio Malvasia, suo mecenate e signore del Castello di Panzano il avvenuta in quell’anno. Fu professore di astronomia all’Università di Bologna e nel 1671 divenne il direttore dell’Osservatorio di Parigi.
 Benedetto CASTELLI (1578 –1643). monaco e matematico, professore, a Pisa, di Bonaventura Cavalieri. Scienziato e benedettino, discepolo e collaboratore di Galileo che egli difese nel processo del 1633 (Galilei nel 1613 gli aveva indirizzato una lettera divenuta presto famosa sui rapporti tra scienza e insegnamento biblico); lettore di matematica dal 1613 a Pisa, tenne poi, dal 1626, la cattedra di quella materia alla Sapienza di Roma. Ebbe larga risonanza la sua opera Della misura delle acque correnti (1628); notevole il suo Discorso sopra la calamita (pubblicato soltanto nel 1883).
Benedetto CASTELLI (1578 –1643). monaco e matematico, professore, a Pisa, di Bonaventura Cavalieri. Scienziato e benedettino, discepolo e collaboratore di Galileo che egli difese nel processo del 1633 (Galilei nel 1613 gli aveva indirizzato una lettera divenuta presto famosa sui rapporti tra scienza e insegnamento biblico); lettore di matematica dal 1613 a Pisa, tenne poi, dal 1626, la cattedra di quella materia alla Sapienza di Roma. Ebbe larga risonanza la sua opera Della misura delle acque correnti (1628); notevole il suo Discorso sopra la calamita (pubblicato soltanto nel 1883).
 Pietro Antonio CATALDI (1552-1626) inventore delle frazioni continue
Pietro Antonio CATALDI (1552-1626) inventore delle frazioni continue
 Bonaventura CAVALIERI (1598-1647), entrò nel 1613 nell’ordine dei Gesuati (da non confondersi con quello dei Gesuiti, che annoverò altri grandi matematici del 500-600).Studiò matematica a Pisa sotto Benedetto Castelli (1578 –1643). Galileo Galilei ne appoggiò la carriera stimandolo uno dei maggiori matematici del suo tempo. Fu l’inventore dell’assonometria cavaliera, e dell’omonimo principio e principalmente il metodo degli indivisibili. La sua prima opera fu Lo specchio ustorio, overo, Trattato delle settioni coniche, con varie applicazioni all’acustica, alla costruzione degli specchi ustori e al moto dei gravi, ove anticipando Galilei (che ne fu irritato) scopre la forma parabolica della traiettoria di un grave.
Bonaventura CAVALIERI (1598-1647), entrò nel 1613 nell’ordine dei Gesuati (da non confondersi con quello dei Gesuiti, che annoverò altri grandi matematici del 500-600).Studiò matematica a Pisa sotto Benedetto Castelli (1578 –1643). Galileo Galilei ne appoggiò la carriera stimandolo uno dei maggiori matematici del suo tempo. Fu l’inventore dell’assonometria cavaliera, e dell’omonimo principio e principalmente il metodo degli indivisibili. La sua prima opera fu Lo specchio ustorio, overo, Trattato delle settioni coniche, con varie applicazioni all’acustica, alla costruzione degli specchi ustori e al moto dei gravi, ove anticipando Galilei (che ne fu irritato) scopre la forma parabolica della traiettoria di un grave.
Ludolph van CEULEN (1540-1610)calcolò pi greco con venti cifre significative.
 Tommaso CEVA (1648 – 1737) è stato un gesuita, poeta e matematico italiano, fu professore di matematica e retorica presso il collegio di Brera, a Milano e fu membro dell’Accademia dell’Arcadia dal 1718. Il suo allievo più famoso fu Giovanni Girolamo Saccheri. Scrisse il poema latino Iesus puer, tradotto in diverse lingue.
Tommaso CEVA (1648 – 1737) è stato un gesuita, poeta e matematico italiano, fu professore di matematica e retorica presso il collegio di Brera, a Milano e fu membro dell’Accademia dell’Arcadia dal 1718. Il suo allievo più famoso fu Giovanni Girolamo Saccheri. Scrisse il poema latino Iesus puer, tradotto in diverse lingue. In ambito matematico si occupò di aritmetica, geometria e gravità, pubblicando gli Opuscola mathematica (1699), ed elaborò uno strumento per dividere l’angolo retto in un dato numero di parti uguali tra loro. Nel 1707 il metodo del Ceva per la polisezione dell’angolo venne pubblicato in Francia da Guillaume de l’Hôpital senza fare alcuna menzione dell’inventore italiano. Il suo libro De natura gravium (Milano, 1669) fu il primo ad introdurre la teoria gravitazionale newtoniana in Italia e contribuì alla sua diffusione.
In ambito matematico si occupò di aritmetica, geometria e gravità, pubblicando gli Opuscola mathematica (1699), ed elaborò uno strumento per dividere l’angolo retto in un dato numero di parti uguali tra loro. Nel 1707 il metodo del Ceva per la polisezione dell’angolo venne pubblicato in Francia da Guillaume de l’Hôpital senza fare alcuna menzione dell’inventore italiano. Il suo libro De natura gravium (Milano, 1669) fu il primo ad introdurre la teoria gravitazionale newtoniana in Italia e contribuì alla sua diffusione.
 Federico COMMANDINO (1509-1575) di Urbino. Si deve a lui una nuova traduzione di alcune opere di Archimede
Federico COMMANDINO (1509-1575) di Urbino. Si deve a lui una nuova traduzione di alcune opere di Archimede (1558, Archimedis Opera nonnulla), tra cui il Trattato dei corpi galleggianti. Tradusse inoltre l’opera di Aristarco da Samo (Su le grandezze e le distanze del Sole e della Luna), la Collezione matematica di Pappo di Alessandria (pubblicata postuma, nel 1588), Euclide (tradotto anche in italiano), i primi quattro libri delle Coniche di Apollonio, pubblicati nel 1566 insieme con il De sectione cylindri di Sereno di Antinoe e i commenti di Eutocio. Tradusse anche alcuni scritti di Tolomeo e di Erone di Alessandria. Curò, insieme a John Dee, la prima edizione a stampa del De superficierum divisionibus liber del matematico iracheno Muhammad al-Baghdadi. fra i suoi allievi vanno ricordati Guidobaldo del Monte e Bernardino Baldi. Commandino fu inoltre in corrispondenza con Francesco Maurolico di Messina, uno dei matematici più creativi del suo tempo. Ha collaborato insieme a Francesco Barozzi.
(1558, Archimedis Opera nonnulla), tra cui il Trattato dei corpi galleggianti. Tradusse inoltre l’opera di Aristarco da Samo (Su le grandezze e le distanze del Sole e della Luna), la Collezione matematica di Pappo di Alessandria (pubblicata postuma, nel 1588), Euclide (tradotto anche in italiano), i primi quattro libri delle Coniche di Apollonio, pubblicati nel 1566 insieme con il De sectione cylindri di Sereno di Antinoe e i commenti di Eutocio. Tradusse anche alcuni scritti di Tolomeo e di Erone di Alessandria. Curò, insieme a John Dee, la prima edizione a stampa del De superficierum divisionibus liber del matematico iracheno Muhammad al-Baghdadi. fra i suoi allievi vanno ricordati Guidobaldo del Monte e Bernardino Baldi. Commandino fu inoltre in corrispondenza con Francesco Maurolico di Messina, uno dei matematici più creativi del suo tempo. Ha collaborato insieme a Francesco Barozzi.
 Christophorus CLAVIUS (1538-1612), noto come Cristoforo Clavio CLAVIO, gesuita, matematico,astronomo.
Christophorus CLAVIUS (1538-1612), noto come Cristoforo Clavio CLAVIO, gesuita, matematico,astronomo.
 August L. CRELLE (1780-1855) noto per i Journal di Crelle, la più antica rivista di matematica.
August L. CRELLE (1780-1855) noto per i Journal di Crelle, la più antica rivista di matematica.
 Giovan Battista DELLA PORTA (1535-1615).
Giovan Battista DELLA PORTA (1535-1615).
 Philippe DE LA HIRE (1640-1718)
Philippe DE LA HIRE (1640-1718)
Agustus DE MOIVRE (1667-1754)
 Girard DESARGUES (1593-1661)
Girard DESARGUES (1593-1661) 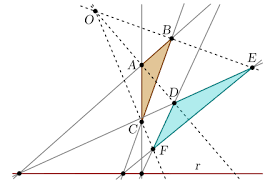
 Giulio Carlo di FAGNANO, Marchese de’ Toschi (1682-1760), di origine marchigiana e autodidatta fu membro della Royal Society di Londra e dell’Accademia delle Scienze di Berlino. Tra le sue opere Produzioni Matematiche stampata a Pesaro nel 1750 e dedicata al Papa Benedetto XIV. Fagnano ha suggerito nuovi metodi di soluzione delle equazioni algebriche di grado 2, 3 e 4. Ha migliorato il lavoro del Rafael Bombelli sui numeri complessi dimostrando che ¶ =2i log [(i-1)/(i+1)] , formula divenuta famosa. Fagnano è famoso è il suo lavoro sui triangoli.
Giulio Carlo di FAGNANO, Marchese de’ Toschi (1682-1760), di origine marchigiana e autodidatta fu membro della Royal Society di Londra e dell’Accademia delle Scienze di Berlino. Tra le sue opere Produzioni Matematiche stampata a Pesaro nel 1750 e dedicata al Papa Benedetto XIV. Fagnano ha suggerito nuovi metodi di soluzione delle equazioni algebriche di grado 2, 3 e 4. Ha migliorato il lavoro del Rafael Bombelli sui numeri complessi dimostrando che ¶ =2i log [(i-1)/(i+1)] , formula divenuta famosa. Fagnano è famoso è il suo lavoro sui triangoli.
 Johan FAULHABER (1580-1635). Fu ingegnere militare, matematico e geometra, fu il primo a pubblicare le tavole logaritmiche di Henry Briggs (1561-1630). La sua opera ha influenzato il giovane Cartesio che lo conobbe personalmente. Nel 1619 pubblicòo il suo lavoro Fama Syderea Nova con le profezie relative alla Grande Cometa del 1618. A lui viene anche attribuito la prima soluzione documentata a mezzo stampa di un temperamento musicale, il temperamento equabile. Nel 1631 pubblicò un’opera, Accademie Algebrae, scritta in tedesco nonostante il titolo in latino, che permetterà a Jacob Bernoulli un matematico nato due decenni dopo la sua morte, di scoprire quella formula che, per il contributo riconosciuto, sarà chiamata formula di Faulhaber. Contemporaneamente coltivò interessi esoterici occupandosi di alchimia, astrologia e numerologia. Si ritiene sia stato un Rosacroce, il famoso ordine segreto, ermetico e cristiano. Le sue previsioni e speculazioni basate su teorie cabalistiche provocarono il malcontento delle autorità ecclesiastiche che, a volte, lo indussero a lasciare Ulma. Collaborò con Keplero e Ludolph van Ceulen. La formula di Faulhaber, in simboli attuali, è la seguente:
Johan FAULHABER (1580-1635). Fu ingegnere militare, matematico e geometra, fu il primo a pubblicare le tavole logaritmiche di Henry Briggs (1561-1630). La sua opera ha influenzato il giovane Cartesio che lo conobbe personalmente. Nel 1619 pubblicòo il suo lavoro Fama Syderea Nova con le profezie relative alla Grande Cometa del 1618. A lui viene anche attribuito la prima soluzione documentata a mezzo stampa di un temperamento musicale, il temperamento equabile. Nel 1631 pubblicò un’opera, Accademie Algebrae, scritta in tedesco nonostante il titolo in latino, che permetterà a Jacob Bernoulli un matematico nato due decenni dopo la sua morte, di scoprire quella formula che, per il contributo riconosciuto, sarà chiamata formula di Faulhaber. Contemporaneamente coltivò interessi esoterici occupandosi di alchimia, astrologia e numerologia. Si ritiene sia stato un Rosacroce, il famoso ordine segreto, ermetico e cristiano. Le sue previsioni e speculazioni basate su teorie cabalistiche provocarono il malcontento delle autorità ecclesiastiche che, a volte, lo indussero a lasciare Ulma. Collaborò con Keplero e Ludolph van Ceulen. La formula di Faulhaber, in simboli attuali, è la seguente:
dove i Numeri Bk sono i numeri di Bernoulli.
 Lodovico FERRARI (1522-1565) (vai a),
Lodovico FERRARI (1522-1565) (vai a),
scopritore della soluzione dell’equazione di quarto grado (1539),
articolo su Ludovico Ferrari (di Giovan Battista Gosio)
 Pierre de FERMAT (1601-1665) è stato un matematico e magistrato francese. Fu tra i principali matematici della prima metà del XVII secolo e dette importanti contributi allo sviluppo della matematica moderna, divulgando una miriade di risultati, spesso senza dimostrazione. Formulò l’ultimo teorema di Fermat la cui dimostrazione è stata fatta da Wiles nel 1993. (vai a)
Pierre de FERMAT (1601-1665) è stato un matematico e magistrato francese. Fu tra i principali matematici della prima metà del XVII secolo e dette importanti contributi allo sviluppo della matematica moderna, divulgando una miriade di risultati, spesso senza dimostrazione. Formulò l’ultimo teorema di Fermat la cui dimostrazione è stata fatta da Wiles nel 1993. (vai a)
Bernard FRENICLE de BESSY (1602-1675) noto per il suo libro “Des quassez ou tables magiques”. Scoprì un numero taxicab (Ta (2) = 1729) e tutti gli 880 quadrati magici differenti di ordine quattro. Sfidò Huygens (1669-1695) a risolvere il seguente sistema diofanteo : x² + y² = z², x² = u² + v², x – y = u – v. Una soluzione fu data da Théophile Pépin (1826 – 1904) solo nel 1880. Ricordiamo che Ta (n) è il più piccolo numero rappresentabile in n modi come somma di due cubi positivi.
 Galileo GALILEI (1564-1642) (vai a)
Galileo GALILEI (1564-1642) (vai a)
Vita e personalità di Galileo Galilei (di Beniamino Segre in Archimede, AnnoXVI n.6 (1964) )
La paternità del principio d’inerzia (di Luca Nicotra, presentato a Science&Philosophy).
Marco GALLI (Bologna, 1645 – 1700) è stato un matematico italiano. La sua opera Miscellaneo matematico è citata come libro raro nel secondo volume de la Biblioteca Italiana di Nicola Francesco Haym.
Giovanna GARZONI(1589-1670) fu un’artista e scienziata italiana. È stata la prima donna a essere ammessa all’Accademia di San Luca di Roma. Garzoni è nota per le sue nature morte e per i suoi studi sul corpo umano.
Pierre GASSENDI (1592-1655) fu filosofo e dal 1645 fu prof. di matematica al Collège Royal. In legami di stretta amicizia con Mersenne, e impegnato in numerose ricerche fisiche (verifica sperimentale della legge galileiana della caduta dei gravi), storico-erudite (dalla ricostruzione della vita e della filosofia di Epicuro alla Notitia Ecclesiae Diniensis, alle vite di Peiresc, di N. Copernico, di T. Brahe). In polemiche filosofiche (contro gli aristotelici, contro R. Fludd, Herbert di Cherbury e R. Cartesio),egli è tra i massimi rappresentanti della nuova scienza e in generale della nuova cultura che si andava affermando nel Seicento: in lui la tradizione storico-erudita di origine umanistica si fonde con precisi interessi scientifici, nella comune prospettiva di edificare una scienza – della natura e degli uomini – condotta “historico sty lo”. Tra le sue opere: Exercitationum paradoxicarum adversus Aristoteleos libri septem (1624) Parhelia (1630); De motu impresso a motore translato (1642); De proportione qua gravia decidentia accelerantur (1646); Institutio astronomica (1647); De vita et moribus Epicuri (1647); Animadversiones in decimum librum Diogenis Laertii qui est de vita, moribus placitisque Epicuri (1649); Philosophiae Epicuri syntagma (1649); Syntagma philosophicum (ed. post. in Opera omnia, 1658).
 Marino GHETALDI, matematico ed astronomo di origine croata. Fu precursore della geometria analitica, usa il + come simbolo di addizione (cfr. Chuquet -1484).
Marino GHETALDI, matematico ed astronomo di origine croata. Fu precursore della geometria analitica, usa il + come simbolo di addizione (cfr. Chuquet -1484).
Albert GIRARD ( 1595 -1633) sembra abbia enunciato il teorema fondamentale dell’algebra” e abbia dato una definizione induttiva per i numeri di Fibonacci. Fu il primo ad usare i simboli sin, cos e tan in un trattato. Ancora Ivan scrisse , nel 1632, che ogni numero primo congruo a 1 mod 4 era la somma di due quadrati in esattamente un unico modo (vedi anche il teorema di Fermat sulle somme di due quadrati). Secondo alcuni storici fu il primo a scoprire le regole per sommare le potenze delle radici di una qualsiasi equazione.
 Christian GOLDBACH (1690-1764) è stato un matematico tedesco, molto noto per la sua congettura sui numeri primi formulata nel 1742 e ancora aperta, asserente che: ogni numero pari da 4 in poi è somma di due primi. Nato nella città di Königsberg figlio di un pastore, Goldbach studiò diritto e matematica e si stabilì in Russia.
Christian GOLDBACH (1690-1764) è stato un matematico tedesco, molto noto per la sua congettura sui numeri primi formulata nel 1742 e ancora aperta, asserente che: ogni numero pari da 4 in poi è somma di due primi. Nato nella città di Königsberg figlio di un pastore, Goldbach studiò diritto e matematica e si stabilì in Russia.
David GREGORY (1659-1708)
Christoph GRIENBERGER (1538-1618), successore di CLAVIUS (1538-1612)
Domenico Guglielmini (1655 – 1710) è stato un matematico, chimico e medico italiano.
 Paolo GULDINO (1577-1643) Teorema di Pappo-Guldino per area e volume delle superficie di rotazione.
Paolo GULDINO (1577-1643) Teorema di Pappo-Guldino per area e volume delle superficie di rotazione.
Thomas HARRIOT (1560 – 1621) è stato un astronomo, traduttore, matematico ed etnografo inglese.
Pierre HERIGONE (1580-1643) latinizzato in Petrus Herigonius. Matematico ed Astronomo, operò a Parigi. Autore di un Cursus mathematicus, (sei volumi1634 -1637); dove utilizzare un simbolismo logico particolare per migliorare lo studio della matematica. Hérigone fu un fautore della notazione.
 Cristiaan HUYGENS (1629-1695) – matematico , fisico , astronomo olandese.
Cristiaan HUYGENS (1629-1695) – matematico , fisico , astronomo olandese.
 Johannes KEPLER (1571-1630) – astronomo e matematico.
Johannes KEPLER (1571-1630) – astronomo e matematico.  Si occupò anche di ottica. La sua legge sul moto dei pianeti è su Astronomia nova del 160.
Si occupò anche di ottica. La sua legge sul moto dei pianeti è su Astronomia nova del 160.
 Gottfried Wilhelm von LEIBNIZ (1646-1716) è stato un filosofo, matematico, scienziato, logico, teologo, linguista, glottoteta, diplomatico, giurista, storico, magistrato tedesco. Interessante il cosiddetto Sogno di Leibniz che nella Dissertatio de arte combinatoria (1666) mise in relazione la sua idea di una mathesis universalis, cioè di una logica concepita come matematica generalizzata. “Secondo ciò — scrive Leibniz — quando sorga una controversia, non ci sarà più necessità di discussione tra due filosofi di quella che c’è tra due calcolatori. Sarà sufficiente prendere una penna, sedersi al tavolo e dirsi l’un l’altro: calcoliamo (calculemus)!”. vedi : profilo di Leibniz Wikipedia.
Gottfried Wilhelm von LEIBNIZ (1646-1716) è stato un filosofo, matematico, scienziato, logico, teologo, linguista, glottoteta, diplomatico, giurista, storico, magistrato tedesco. Interessante il cosiddetto Sogno di Leibniz che nella Dissertatio de arte combinatoria (1666) mise in relazione la sua idea di una mathesis universalis, cioè di una logica concepita come matematica generalizzata. “Secondo ciò — scrive Leibniz — quando sorga una controversia, non ci sarà più necessità di discussione tra due filosofi di quella che c’è tra due calcolatori. Sarà sufficiente prendere una penna, sedersi al tavolo e dirsi l’un l’altro: calcoliamo (calculemus)!”. vedi : profilo di Leibniz Wikipedia.
vedi: Domenico Marconi (2009). Gottfried Wilhelm Leibnitz (1646-1716), Prodromi dell’informatica e mutamenti nel pensiero scientifico nelle sue opere e nel suo tempo, pp 1-87. Rielaborazione per il sito www.afsu.it dell’ACCADEMIA DI FILOSOFIA DELLE SCIENZE UMANE della Tesi di Dottorato in “Epistemologia dell’Informatica e mutamenti Sociali” discussa dal Prof. Ing. Domenico Marconi, nel Giugno 2009, nell’Università di Teramo con titolo omonimo, Relatore il Prof. Franco Eugeni, correlatore il Prof. Ezio Sciarra. (Tratta anche del simbolismo matematico moderno). vedi anche: F.Eugeni – R. Mascella, Memoria e lingua artificiale …, in: R.S.Borrello-L.Nicotra (2010, a cura di) Il Drago e la farfalla, Universitalia, Roma (Dalla comunità di Matteo Ricci alla numerazione binaria e al computer di Leibniz).
 Colin MACLAURIN (1698-1746) Serie di Maclaurin
Colin MACLAURIN (1698-1746) Serie di Maclaurin
Matteo MAINARDI (XVI sec). Viene ricordato per aver fatto, insieme con Antonio Maria Villavec-chia, Ambrogio Lerici, Giovanni Domenico Peri, Simon Grisogono, Giovanni Antonio Moschetti, Lodovico Flori e altri la storia della ragioneria nel seicento italiano, scrivendo varie opere sul tema, oltre a un’opera sulla storia di tutte le chiese di Bologna; tutte le sue opere furono ristampate nel 1700. La sua opera del 1632 La scrittura mercantile formatamente regolata è ritenuta particolarmente rilevante.
 Giovanni MAGINI (1555- 1617), noto come Maginus, è stato un astronomo, matematico e cartografo, si laureò in filosofia a Bologna il 10 giugno 1579. Si dedicò prestissimo agli studi astronomici; del 1582 sono infatti le sue Ephemerides coelestium motuum (trad. in italiano nel 1583), dell’anno stesso i trattati astronomici intitolati Delle introdottioni, del 1585 le Tabulae secundorum mobilium coelestium. Salito per queste e altre opere in alta fama, fu eletto il 4 agosto 1588 alla cattedra pomeridiana di matematica già tenuta nello Studio di Bologna da Ignazio Danti (1536-1586), essendo stato preferito a Galileo.
Giovanni MAGINI (1555- 1617), noto come Maginus, è stato un astronomo, matematico e cartografo, si laureò in filosofia a Bologna il 10 giugno 1579. Si dedicò prestissimo agli studi astronomici; del 1582 sono infatti le sue Ephemerides coelestium motuum (trad. in italiano nel 1583), dell’anno stesso i trattati astronomici intitolati Delle introdottioni, del 1585 le Tabulae secundorum mobilium coelestium. Salito per queste e altre opere in alta fama, fu eletto il 4 agosto 1588 alla cattedra pomeridiana di matematica già tenuta nello Studio di Bologna da Ignazio Danti (1536-1586), essendo stato preferito a Galileo.
Eustacchio MANFREDI (1674-1739). Si occupò di molti argomenti in vari settori. Per le seguendo soprattutto Guglielmini. Questi formò anche Gabriele Manfredi, Stancari e G. Verzaglia (tra i primi cultori italiani di analisi, mentre il M. ammise di avere curato poco l’algebra; andò poco oltre i mezzi classici dell’astronomia di posizione e non contribuì alla meccanica celeste: nel 1716 scrisse che nei Principia Newton sembrava “parlare arabico”). Il restauro della meridiana nella basilica di S. Petronio curato da G.D. Cassini e Guglielmini nel 1695 spinse il M. e Stancari a compiervi osservazioni (dati ibid., b. 3). Passato Guglielmini a Padova, nel 1699 l’Università di Bologna destinò una terza lettura di matematica ai settori prima curati da lui, e il M. l’ottenne. Tuttavia la scarsa retribuzione gli lasciò i problemi finanziari, mentre la monacazione della Vandi lo colpì nell’intimo. Alle difficoltà materiali fece fronte con aiuti (in particolare di Orsi) e accettando incarichi che assorbirono poi molte delle sue forze. Nei corsi seguì un ciclo triennale (Euclide, teoria dei pianeti, Alma-gesto). Forse, però, sotto i nomi antichi offrì anche contenuti nuovi: lezioni del 1703 s’intitolano Tractatus analyticus e Rudimenta analysis speciosae (Bologna, Biblioteca universitaria, Mss. aggiunti, 4318); lezioni di astronomia e altro (Ibid., Mss. italiani, 654, nn. 1, 3, 5); Institutiones geographicae nella Biblioteca apostolica Vaticana (Ferrajoli, 52). Questi testi potrebbero però riferirsi a un insegnamento privato, comune nell’epoca, perché allievi del M. ebbero competenze più ampie di quelle fornite dai corsi pubblici.
 Simon MARIUS (1573-1624)
Simon MARIUS (1573-1624)

Gerard MERCATOR (1512-1594) vedi Nicolaus M. (1620-1687)
Nicolaus MERCATOR (1620-1687) da non confondere con Gerard (il cartografo)
Pietro MENGOLI (1626-1686) è stato un matematico italiano. Studiò con Bonaventura Cavalieri e gli subentrò nell’insegnamento della matematica nell’Università di Bologna. I suoi studi si collocano a mezza via tra il metodo degli indivisibili di Cavalieri e quelli di Leibniz e Newton. Scrisse, fra l’altro, i Geometriae speciosae elementa (1659), anticipando Cauchy relativamente al concetto di limite e di integrale definito.
Maria Sibylla MERIAN (1647-1717) – Artista, naturalista e illustratrice tedesca. È nota per i suoi studi sui lepidotteri e per aver contribuito alla fondazione dell’entomologia moderna.
 Marin MERSENNE (1558-1649)
Marin MERSENNE (1558-1649)
George MOHR (1640-1697) alias Morendal, matematico danese, Si recò nei Paesi Bassi nel 1662 per studiare matematica sotto la guida di Christiaan Huygens. Prima di tornare nella natia Danimarca, studiò in Francia e Inghilterra. Era un matematico pressoché sconosciuto nel suo tempo. Scrisse Euclides Danicus nel 1672, dove dimostra che tutte le costruzioni euclidee eseguibili con riga e compasso, possono essere fatte con l’utilizzo del solo compasso. Anticipò in questo Lorenzo Mascheroni che sarebbe giunto alle medesime conclusioni 125 anni più tardi, il risultato è noto come Teorema di Mascheroni-Mohr.
 Abraham de MOIVRE (1667-1754). È noto per la formula di de Moivre (che collega numeri complessi e trigonometria), i suoi lavori sulla distribuzione normale e la teoria della probabilità, e per la scoperta (in forma incompleta) della formula di approssimazione di Stirling. Quest’ultima venne usata nel 1733 da de Moivre per derivare la variabile casuale normale come una approssimazione della variabile casuale binomiale. Nella seconda edizione, pubblicata nel 1738 de Moivre accreditò a James Stirling i miglioramenti apportati. Poco più che ventenne si trasferì a Londra, dove strinse amicizia con Edmund Halley e Isaac Newton. A 30 anni venne ammesso alla Royal Society. Il giurista britannico Francis Maseres, anch’egli membro della Royal Society, nel suo The principles of the doctrine of life-annuities (1783) si basò sulle tavole di De Moivre e Deparcieux. Nell’ultimo periodo della sua vita soffrì di letargia e secondo un aneddoto avrebbe predetto la data della sua morte servendosi di un calcolo matematico. Infatti, notando che dormiva 15 minuti in più ogni giorno, suppose che sarebbe morto quando il sonno avesse raggiunto le 24 ore, precisamente il 27 novembre 1754.
Abraham de MOIVRE (1667-1754). È noto per la formula di de Moivre (che collega numeri complessi e trigonometria), i suoi lavori sulla distribuzione normale e la teoria della probabilità, e per la scoperta (in forma incompleta) della formula di approssimazione di Stirling. Quest’ultima venne usata nel 1733 da de Moivre per derivare la variabile casuale normale come una approssimazione della variabile casuale binomiale. Nella seconda edizione, pubblicata nel 1738 de Moivre accreditò a James Stirling i miglioramenti apportati. Poco più che ventenne si trasferì a Londra, dove strinse amicizia con Edmund Halley e Isaac Newton. A 30 anni venne ammesso alla Royal Society. Il giurista britannico Francis Maseres, anch’egli membro della Royal Society, nel suo The principles of the doctrine of life-annuities (1783) si basò sulle tavole di De Moivre e Deparcieux. Nell’ultimo periodo della sua vita soffrì di letargia e secondo un aneddoto avrebbe predetto la data della sua morte servendosi di un calcolo matematico. Infatti, notando che dormiva 15 minuti in più ogni giorno, suppose che sarebbe morto quando il sonno avesse raggiunto le 24 ore, precisamente il 27 novembre 1754.
 Pierre Remonde de MONTMORT (1687-1719), famoso per il suo Essays d’analyse sue le jeux d’azard (1708), preludio al 1759)calcolo delle probabilità. Noto anche per i suoi studi pionieristici sulle differenze finite e per una sua opera sul calcolo delle probabilità. (vedi Montucla 1700)
Pierre Remonde de MONTMORT (1687-1719), famoso per il suo Essays d’analyse sue le jeux d’azard (1708), preludio al 1759)calcolo delle probabilità. Noto anche per i suoi studi pionieristici sulle differenze finite e per una sua opera sul calcolo delle probabilità. (vedi Montucla 1700)
 Pierre-Louis Moreau de Malpertuis (1698 – 1759). Inizialmente musicista, pubblicò il suo primo lavoro Sur la forme des instruments de musique . Seguirono lavori matematici sulle curve, si interessò anche di biologia e pubblicò un saggio sulle salamandre. Nel 1728 visitò Londra e fu eletto fellow della Royal Society. Per approfondire le sue conoscenze scientifiche si recò a Basilea per studiare con Johann Bernoulli presso il quale abitava. Qui apprese la teoria dei vortici di Cartesio, la meccanica di Leibniz, la fisica di Newton per la teoria della gravitazione. Si laureò a Basilea nel 1729.Al ritorno a Parigi scrisse vari lavori di meccanica e di astronomia tra cui uno sui corpi in rotazione nel quale discute sulla natura degli anelli di Saturno e sulla forma di un corpo in rotazione, interessante anche se contiene errori.
Pierre-Louis Moreau de Malpertuis (1698 – 1759). Inizialmente musicista, pubblicò il suo primo lavoro Sur la forme des instruments de musique . Seguirono lavori matematici sulle curve, si interessò anche di biologia e pubblicò un saggio sulle salamandre. Nel 1728 visitò Londra e fu eletto fellow della Royal Society. Per approfondire le sue conoscenze scientifiche si recò a Basilea per studiare con Johann Bernoulli presso il quale abitava. Qui apprese la teoria dei vortici di Cartesio, la meccanica di Leibniz, la fisica di Newton per la teoria della gravitazione. Si laureò a Basilea nel 1729.Al ritorno a Parigi scrisse vari lavori di meccanica e di astronomia tra cui uno sui corpi in rotazione nel quale discute sulla natura degli anelli di Saturno e sulla forma di un corpo in rotazione, interessante anche se contiene errori.
Nel 1732 si dichiara un sostenitore delle teorie Newtoniane col trattato Figures des astres (La forma dei corpi celesti) dove espone la sua idea sulla forma della Terra, uno dei principali problemi oggetto di disputa all’epoca.
Nel 1735 l’Accademia di Parigi inviò una spedizione in Perù, guidata da La Condamine per compiere misure del grado di meridiano, e una seconda spedizione fu inviata in Lapponia sotto la guida di Maupertuis con lo stesso compito.
Isaac NEWTON (1643-1727)
 Jacques OZANAM (16 giugno 1640 –1718)
Jacques OZANAM (16 giugno 1640 –1718)
 Blaise PASCAL (1623-1662). è stato
Blaise PASCAL (1623-1662). è stato  un matematico, fisico, filosofo e teologo francese. Bambino prodigio, fu istruito dal padre.
un matematico, fisico, filosofo e teologo francese. Bambino prodigio, fu istruito dal padre.
Elena Lucrezia Cornaro PISCOPIA (1646-1684) – Filosofa, matematica e scienziata italiana. È stata la prima donna ad essere laureata in filosofia all’Università di Padova.
Jacques-Charles PELETIER du Mons (1517-1582)
John PLAYFAIR (1748 – 1819) è stato un matematico e filosofo scozzese. Il libro di testo di Playfair Elementi di Geometria è famoso, specialmente nella letteratura anglosassone, per la riformulazione dell’assioma euclideo relativo alle parallele noto ora come assioma di Playfair (1795). Fu segretario generale della Royal Society di Edimburgo.
 Giovan Battista della PORTA (1535-1615), enciclopedico, in particolare crittografo.
Giovan Battista della PORTA (1535-1615), enciclopedico, in particolare crittografo.
Ramiro RAMPINELLI (1697-1795) bresciano, fu con Jacopo Francesco RICCATI (1676-1754) maestro di Vincenzo Riccati (1707-1775).
Robert RECORDE (?1512 -1558) matematico e medico gallese, considerato il fondatore della scuola matematica inglese, è stato il primo ad utilizzare il segno grafico = (uguale) nel suo trattato di algebra “The Whetstone of Witte”, il primo edito in Inghilterra (1557). Si utilizzava “uguale a”. Utilizza la parola Zenzizenzizenzic , notazione matematica obsoleta che indica l’ottava potenza di un numero, ovvero . Deriva dalla parola tedesca zenzic analoga al «censo di censo» adoperata, da Leonardo Fibonacci (1170– 1242) nel suo Liber abbaci per indicare la potenza alla quarta, ovvero .
Jacopo Francesco RICCATI (1676-1754), conte di un ramo della famosa famiglia romana COLONNA, ramo trapiantato in Veneto nel sec. XV. Padre di Giordano e Vincenzo anche loro matematici. Noto per la soluzione dell’equazione differenziale y’ = a(x) + b(x) y + c(x) y2 , che porta il suo nome e che non risolubile per vie elementari.
 Matteo RICCI (1552-1610). E’ stato un gesuita, matematico, cartografo e sinologo italiano. È stato proclamato Servo di Dio il 19 aprile 1984. Vissuto al tempo della dinastia Ming, padre Matteo Ricci ha impresso un forte impulso all’azione evangelizzatrice ed è riconosciuto come uno dei più grandi missionari della Cina. Vedi: F.Eugeni-R.Mascella, Memoria e lingua artificiale: gli scambi tra Europa e Cina, in:(a cura di L.Nicotra e R.Salina Borello,(2009).Il Drago e la farfalla, Universitalia -Roma).
Matteo RICCI (1552-1610). E’ stato un gesuita, matematico, cartografo e sinologo italiano. È stato proclamato Servo di Dio il 19 aprile 1984. Vissuto al tempo della dinastia Ming, padre Matteo Ricci ha impresso un forte impulso all’azione evangelizzatrice ed è riconosciuto come uno dei più grandi missionari della Cina. Vedi: F.Eugeni-R.Mascella, Memoria e lingua artificiale: gli scambi tra Europa e Cina, in:(a cura di L.Nicotra e R.Salina Borello,(2009).Il Drago e la farfalla, Universitalia -Roma).
 Giovan Battista RICCIOLI (1598-1671) Matematico , astronomo , gesuita costruisce un suo sistema ed è fautore del geocentrismo. Scrive il Nuovo Almagesto.
Giovan Battista RICCIOLI (1598-1671) Matematico , astronomo , gesuita costruisce un suo sistema ed è fautore del geocentrismo. Scrive il Nuovo Almagesto.
Geminiano RONDELLI (1652-1739), Modena. Conseguì la laurea in filosofia nell’Università di Bologna il 4 agosto 1687, dopo avere svolto, dal 1680, incarichi di lettore straordinario di filosofia e di astronomia. Il suo maestro più importante fu il matematico Pietro Mengoli. Nel 1680 conseguì il diaconato e il presbiterato. Dal 1689 al 1697-98 ricoprì il ruolo di lettore di matematica nello Studio bolognese, con il compito di spiegare ad anni alterni la matematica di Euclide e l’astronomia di Tolomeo. I testi di evidente finalità didattica da lui pubblicati dal 1684 . Dal dicembre 1698 gli fu assegnata, in sostituzione di Domenico Guglielmini, trasferitosi a Padova, la lettura di idrometria, di cui restò titolare . Rondelli scrisse un Trattato idrometrico pratico, di ben 386 pagine e corredato di tavole, conservato all’Archiginnasio di Bologna, dove affronta «l’enigma forza/pressione» ma scrive «vistose contraddizioni». Grazie alla sua intermediazione, intorno al 1712 cominciò a prestare i suoi servizi alla stessa Repubblica anche un suo più giovane collega bolognese, Eustachio Manfredi (1674-1739), lettore di matematica dall’inizio del secolo ed esperto di problemi idraulici. La partecipazione di Rondelli al processo di rinnovamento della cultura scientifica e della pratica sperimentale che caratterizzò Bologna dall’inizio del XVIII secolo fu indubbiamente consistente, anche se meno lineare di quella di altri protagonisti. Nel 1705 entrò a far parte dell’Accademia degli Inquieti, fondata da Eustachio Manfredi nel 1690 e rilanciata l’anno precedente dall’elezione di un nuovo ‘principe’, il futuro grande anatomico Giovanni Battista Morgagni, allora studente a Bologna e assiduo frequentatore del suo insegnamento privato di matematica.
 Gilles Personier de ROVERVAL (1602-1675) è stato un matematico e fisico francese, ebbe lacattedra di matematica al Collège Royal. Fu uno dei precursori del calcolo infinitesimale; fra l’altro si occupò della determinazione delle tangenti e del calcolo di aree. Affermò di aver ideato per primo il metodo degli indivisibili, ma il suo Traité des indivisibles è di vari anni successivo alla Geometria di Bonaventura Cavalieri. Fu anche in polemica con Evangelista Torricelli, rivendicando la priorità della quadratura della cicloide. Articolo: S.Nicotra (1961. La circonferenza di Roberval, La Scienza e i giovani, (suppl. Archimede), n.2.
Gilles Personier de ROVERVAL (1602-1675) è stato un matematico e fisico francese, ebbe lacattedra di matematica al Collège Royal. Fu uno dei precursori del calcolo infinitesimale; fra l’altro si occupò della determinazione delle tangenti e del calcolo di aree. Affermò di aver ideato per primo il metodo degli indivisibili, ma il suo Traité des indivisibles è di vari anni successivo alla Geometria di Bonaventura Cavalieri. Fu anche in polemica con Evangelista Torricelli, rivendicando la priorità della quadratura della cicloide. Articolo: S.Nicotra (1961. La circonferenza di Roberval, La Scienza e i giovani, (suppl. Archimede), n.2.
Giovan Battista ROFFENI (1585-1643) astromo
 Adrian VAN ROOMEN (1561-1615) italianizzato in Adriano Romano, matematico ed astronomo. Pubblicò il trattato Archimedis circuli dimensionem exposito et analysis (1597), nel quale diede le prime 16 cifre decimali di pi greco, un record per quel tempo. Calcolò a tale scopo, seguendo Archimede, il perimetro di poligoni inscritti e circoscritti di 230 lati. Nel 1602 pubblicò il trattato Chordarum arcubus circuli primarilis, quibus videlicet is in triginta dirimitur partes, subtensarum resolutio, nel quale vengono calcolate molte radici atte ad esprimere la lunghezza dei lati di molti poligoni regolari. Partendo da tali dati pubblicò tavole con i valori della funzione seno con 9 decimali. OPERA. Universae mathesis idea, Herbipoli, Georg Fleischmann, 1602.
Adrian VAN ROOMEN (1561-1615) italianizzato in Adriano Romano, matematico ed astronomo. Pubblicò il trattato Archimedis circuli dimensionem exposito et analysis (1597), nel quale diede le prime 16 cifre decimali di pi greco, un record per quel tempo. Calcolò a tale scopo, seguendo Archimede, il perimetro di poligoni inscritti e circoscritti di 230 lati. Nel 1602 pubblicò il trattato Chordarum arcubus circuli primarilis, quibus videlicet is in triginta dirimitur partes, subtensarum resolutio, nel quale vengono calcolate molte radici atte ad esprimere la lunghezza dei lati di molti poligoni regolari. Partendo da tali dati pubblicò tavole con i valori della funzione seno con 9 decimali. OPERA. Universae mathesis idea, Herbipoli, Georg Fleischmann, 1602.
Girolamo SACCHERI (1667-1733), entrò diciottenne nell’ordine della Compagnia di Gesù a Genova, dove fu avviato allo studio della geometria. Insegnò filosofia, matematica e teologia nei collegi gesuiti di Torino e di Pavia. Nel 1697 pubblicò un trattato di logica,nel 1708 un trattato di statica. Nel 1733, l’anno della sua morte, uscì l’opera di maggiore importanza : “Euclides ab omni nævo vindicatus” (Euclide riscattato da ogni difetto).
NOTA. L’opera di Saccheri fu tradotta in inglese da G.B. Halsted (1894) , on tedesco da Engel e STACKEL (1895) e in italiano da G. BOCCARDINI (1904).
Giuseppe Giusto SCALIGERO (1540-1609). Costruisce il calendario giuliano.
Frans van SHOOTEN (1615-1660) . – Matematico Fu maestro di C. Huygens all’univ. di Leida. Curò la pubblicazione delle opere matematiche di F. Viète (1646), tradusse in latino e commentò la Géométrie di Descartes (1649). Autore di Exercitationum mathematicarum libri quinque (1657).
Robert SIMSON (1687-1768) matematico scozzese. Sia P un qualsiasi punto di una circon-ferenza circoscritta ad un triangolo, i piedi delle perpendicolari condotte da P ai lati del triangolo sono allineati. La retta che passa per questi tre punti è chiamata Retta di Simson . La dimostrazione del teorema legato a tale retta è però da attribuirsi a William Wallace che la formulò nel 1797. Il segmento individuato sulla retta è un caso degenere di triangolo pedale. L’involuzione delle rette di Simson definisce un deltoide chiamato deltoide di Steiner.
Vellebrord van Rojen SNELL (1581-1626) Snellius. Scrisse Erathostenes Batavus.
 Simon STEVIN (1548-1620), Stevino. E’ stato un ingegnere, fisico e matematico fiammingo. Si stabilì nella Repubblica delle Sette Province Unite, dove lavorò come ingegnere idraulico nella progettazione e costruzione di dighe e canali e dove fu intendente generale dei lavori pubblici. In campo matematico, a Stevin è dovuta l’introduzione di una nuova notazione per i numeri decimali, che permetteva di estendere a tali numeri le normali operazioni algebriche sui numeri interi, anziché usare la notazione frazionaria. L’innovazione di Stevin (1585) ha aperto la strada alla notazione decimale moderna e al concetto di “numero reale”. Pubblicò 11 volumi. La legge di Stevino sui fluidi incomprimibili è p = ρ gh , che permette di calcolare la pressione p esistente ad ogni profondità entro una colonna di fluido, dove h è la profondità del punto considerato, conoscendo la densità ρ del liquido stesso, mentre g è l’accelerazione di gravità (nel caso della terra: 9,8 m/s).
Simon STEVIN (1548-1620), Stevino. E’ stato un ingegnere, fisico e matematico fiammingo. Si stabilì nella Repubblica delle Sette Province Unite, dove lavorò come ingegnere idraulico nella progettazione e costruzione di dighe e canali e dove fu intendente generale dei lavori pubblici. In campo matematico, a Stevin è dovuta l’introduzione di una nuova notazione per i numeri decimali, che permetteva di estendere a tali numeri le normali operazioni algebriche sui numeri interi, anziché usare la notazione frazionaria. L’innovazione di Stevin (1585) ha aperto la strada alla notazione decimale moderna e al concetto di “numero reale”. Pubblicò 11 volumi. La legge di Stevino sui fluidi incomprimibili è p = ρ gh , che permette di calcolare la pressione p esistente ad ogni profondità entro una colonna di fluido, dove h è la profondità del punto considerato, conoscendo la densità ρ del liquido stesso, mentre g è l’accelerazione di gravità (nel caso della terra: 9,8 m/s).
 Brook TAYLOR (1685-1731) serie di Taylor
Brook TAYLOR (1685-1731) serie di Taylor
 Evangelista TORRICELLI(1608-1647)
Evangelista TORRICELLI(1608-1647)
Jean TRENCHANT (… – XV secolo) è stato un matematico francese. La sua opera principale L’aritmetique departie en trois livres è citata come fonte da Simone Stevino nella prefazione delle sue Tafelen van Interest. (FR) Jean Trenchant, L’aritmetique de Jan Trenchant departie en trois livres, ensemble un petit discours des changes. Avec l’art de calculet aux Getons, Lyon, Jove, 1561. (FR) Jean Trenchant, Arithmetique, A Lyon, Michel Jouve, Pierre Roussin, 1571.
 Luca VALERIO (1552-1618) fu chiamato da Galileo “il nuovo Archimede”. Fu uno dei più interessanti esponenti della matematica italiana del tardo XVI secolo, nacque a Napoli nel 1552, figlio del cuoco ferrarese, Giovanni Valeri, e di Giovanna Rodomano di Corfù città dove fu allevato. QA 17 anni entrò nella Compagnia di Gesù e fu a Roma dal 1570. Studiò al Collegio Romano, sotto Cristoforo Clavio, logica, matematica e greco classico. Fu lui a scoprire il calcolo del volume della sfera tramite la famosa scodella, attribuita a Galileo. Vai a: Luca Nicotra:: Leggendo Galileo: dalla scodella di Luca Valerio agli indivisibili di Bonaventura Cavalieri e all’Additive Manufacturing, in: Per. di Matematica (2022), serie IV, vol. IV (1), p.p. 7-35.
Luca VALERIO (1552-1618) fu chiamato da Galileo “il nuovo Archimede”. Fu uno dei più interessanti esponenti della matematica italiana del tardo XVI secolo, nacque a Napoli nel 1552, figlio del cuoco ferrarese, Giovanni Valeri, e di Giovanna Rodomano di Corfù città dove fu allevato. QA 17 anni entrò nella Compagnia di Gesù e fu a Roma dal 1570. Studiò al Collegio Romano, sotto Cristoforo Clavio, logica, matematica e greco classico. Fu lui a scoprire il calcolo del volume della sfera tramite la famosa scodella, attribuita a Galileo. Vai a: Luca Nicotra:: Leggendo Galileo: dalla scodella di Luca Valerio agli indivisibili di Bonaventura Cavalieri e all’Additive Manufacturing, in: Per. di Matematica (2022), serie IV, vol. IV (1), p.p. 7-35.
 Francois VIETE (1540-1833) Scrisse In artem analyticam isagoge. Interessante la sua notazione , adottata da Cartesio, che prelude all’attuale pur non coincidendo con essa. Approfondì la Trigonometria piana e sferica e si occupò di Astronomia.
Francois VIETE (1540-1833) Scrisse In artem analyticam isagoge. Interessante la sua notazione , adottata da Cartesio, che prelude all’attuale pur non coincidendo con essa. Approfondì la Trigonometria piana e sferica e si occupò di Astronomia.
 William WALLACE (1768-1843) allievo del fisico John Robison (1739– 1805) e del matematico John Playfair (1748 – 1819) del quale fu successore nella cattedra di Edimburgo, tra i suoi allievi tra i suoi allievi vi fu l’astronoma Mary Somerville (1780-1872). Dimostrò l’esistenza della retta di Simson (1687-1768). Nel 1807 dimostrò un risultato sui poligoni equivalenti che divenne in seguito conosciuto come il teorema di Bolyai-Gerwien-Wallace asserente che: Due poligoni aventi la stessa area sono equiscomponibili, ossia possono essere suddivisi in un numero finito di parti a due a due congruenti.
William WALLACE (1768-1843) allievo del fisico John Robison (1739– 1805) e del matematico John Playfair (1748 – 1819) del quale fu successore nella cattedra di Edimburgo, tra i suoi allievi tra i suoi allievi vi fu l’astronoma Mary Somerville (1780-1872). Dimostrò l’esistenza della retta di Simson (1687-1768). Nel 1807 dimostrò un risultato sui poligoni equivalenti che divenne in seguito conosciuto come il teorema di Bolyai-Gerwien-Wallace asserente che: Due poligoni aventi la stessa area sono equiscomponibili, ossia possono essere suddivisi in un numero finito di parti a due a due congruenti.
 John WALLIS (1616-1703) è stato un presbitero e matematico inglese, ha contribuito allo sviluppo del calcolo infinitesimale. Tra il 1643 e il 1689 è stato capo crittografo del Parlamento del Regno Unito e successivamente della corte reale.
John WALLIS (1616-1703) è stato un presbitero e matematico inglese, ha contribuito allo sviluppo del calcolo infinitesimale. Tra il 1643 e il 1689 è stato capo crittografo del Parlamento del Regno Unito e successivamente della corte reale.
 Cristopher WREN (1623-1723). Architetto famoso per la ricostruzione di Londra dopo l’incendio del 1666, in particolare la cattedrale di St Paul e l’Osservatorio di Greenwich. Membro della Royal Society. Si occupò di tematiche di elasticità e problemi d’urto. Dimostrò che l’iperboloiide di rotazione ad 1 falda è una superficie rigata, lprovando che si ottiene facendo ruotare una retta sghemba con l’asse attorno ad essa; calcolò la lunghezza dell’arco di cicloide. Fu Gran Maestro della Massoneria operativa in una Gran Lpoggia che operava prima del 1717.
Cristopher WREN (1623-1723). Architetto famoso per la ricostruzione di Londra dopo l’incendio del 1666, in particolare la cattedrale di St Paul e l’Osservatorio di Greenwich. Membro della Royal Society. Si occupò di tematiche di elasticità e problemi d’urto. Dimostrò che l’iperboloiide di rotazione ad 1 falda è una superficie rigata, lprovando che si ottiene facendo ruotare una retta sghemba con l’asse attorno ad essa; calcolò la lunghezza dell’arco di cicloide. Fu Gran Maestro della Massoneria operativa in una Gran Lpoggia che operava prima del 1717.


