torna a Periodi della Matematica. torna a Periodi della Fisica
torna a Periodi dell’Astronomia torna Periodi della Filosofia
Dall’Antichità al 1.000
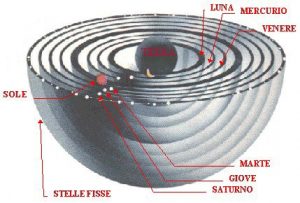
Le sfere concentriche dell’universo di Eudosso e Archimede
Una visione generale delle scienze fino all’anno 1.000: presentiamo una ministoria dell’astronomia e quindi della matematica del tempo, ministoria che nella all’ora reatà non può essere disgiunta nemmeno dalla filosofia. (vai a Ministoria dell’astronomia).
La filosofia antica si sviluppa in area mediterranea nella Grecia antica in un lungo arco di tempo, che va dall’ VIII secolo a.C., con la scuola di Mileto, ma che si specializza nel VI secolo con i naturalisti ionici (Talete, Anassimandro e Anassimene) fino ai capisaldi della filosofia antica, come Socrate, Platone e Aristotele, per continuare fino al I secolo a.C., con la filosofia di Ipparco del II secolo fino a Vitruvio del I Secolo.
VIII secolo a.C. (800-701)
BAUDHAYANA (800 a.C.circa) Antichissimo maestro indiano e caposcuola, al pari di Āpastamba, nell’ambito di dottrine religiose che si ricongiungono allo Yajurveda nero. E’ stato un matematico e filosofo indiano. Studioso dello Yajurveda nero, gli si devono diversi sutra e varie dimostrazioni geometriche. Approntò inoltre un metodo di calcolo della radice quadrata di 2 corretto fino alla 5ª cifra decimale.
Antichità fino all’anno mille
VII secolo a.C. (700-601)
VI secolo a.C. (600-501)
PRESOCRATICI e PRESOFISTI (VI sec -450a.C). Sono un interessante gruppo di pensatori, anteriori a Socrate (470-399 a.C.), che si sono occupati del problema della natura a della realtà, e sono stati i primi che hanno spostato il centro della riflessione filosofica dall’universo all’uomo. Essi furono: Talete (fine VII – prima metà VI), Anassimandro (610/609 – 547/546), Pitagora (580/570- 495 a.C. circa) , Eraclito di Efeso (535 – 475 a.C.), Parmenide (550 – 450).
ANASSIMANDRO di MILETO (610 – 546 a.C.) Filosofo presocratico, fu membro della Scuola di Mileto e allievo di Talete. Fu maestro di Anassimene. Anassimandro fu uno dei primi sostenitori della scienza e cercò di osservare e spiegare diversi aspetti dell’universo, con un particolare interesse per le sue origini, sostenendo che la natura sia governata da leggi, proprio come le società umane, e tutto ciò che disturba l’equilibrio non può continuare a lungo. In astronomia, tentò di descrivere la meccanica dei corpi celesti in relazione alla Terra. In fisica, la sua postulazione che l’indefinito (o Ápeiron) fosse la fonte di tutte le cose, cioè che tutto fosse fatto di apeiron o qualcosa di indefinito piuttosto che qualcosa di specifico. Spinse la filosofia greca a un nuovo livello di astrazione concettuale. La sua conoscenza della geometria gli permise di introdurre lo gnomone in Grecia. Realizzò una mappa del mondo grazie alla quale contribuì notevolmente al progresso della geografia.
PARMENIDE (540-470 a.C.)
PITAGORA di Samo (569-475 a.C.).
TALETE (Thales) di MILETO (624-548 a.C.) Oltre che primo filosofo, presocratico, e fondatore della scuola di Mileto, Talete era un ottimo astronomo e si narra che abbia predetto un’eclissi solare. Circa l’Universo propose che propose che tutto fosse fatto d’acqua, forse non andando lontano da certe realtà futura. Fu Maestro d Anassimandro che a sua volta fu allievo di Anassimene l’ultimo della Scuola di Mileto. Era, inoltre, un valente geometra, e a lui si attribuisce un primo calcolo dell’altezza delle piramidi misurando la loro ombra, cosa piuttosto credibile per via del ben noto Teorema di Talete : Date tre rette parallele, tagliate da due rette trasversali, il rapporto tra i segmenti omologhi dell’una e dell’altra è sempre costante. L’enunciazione di questo teorema, si ritiene fossero già conosciute ai tempi degli antichi babilonesi. (scheda profilo e T. inverso di Talete, di G. Vaona (1920) e F. Eugeni).
V secolo a.C. (500-401)
Troviamo quali tardivi pre-socratici Zenone di Elea (489– 431 a.C.), Democrito (460-360 a.C.), i Sofisti (dalla 2° metà del V Sec.) e Protagora (490 – 415/411 a.C.) .
“Sofista è chi, facendo uso di ragionamenti capziosi, da un lato cerca di indebolire e offuscare il vero e dall’altro tenta di rafforzare il falso, rivestendolo delle apparenze del vero.
- ofisti della prima generazione sono : Protagora, Gorgia da Lentini (483 – 375 a. C.).o, Prodico e Ippia.
- Sofisti della seconda generazione, solitamente allievi dei primi, Antifonte, Crizia, Trasimaco, Licofrone, Callicle, Alcidamante, Polo, l’Anonimo di Giamblico.
Nel 387 a.C. Platone (427-347) fondò la celebre scuola filosofica, detta Accademia. La data non è del tutto certa. A quanto narrano gli storici successivi Filodemo di Gadara (110 -35 a.C) ,e Diogene Laerzio (180- 240 d-C.) Platone la fondò al ritorno dai suoi viaggi in Sicilia, dopo aver abbandonato Siracusa in seguito a contrasti con il tiranno Dionisio il Vecchio. All’inizio del -V secolo a.C. l’Accademia diviene la Scuola di Atene: Platone, Eudosso di Cnido, creatore insieme con Antifonte, del metodo di esaustione ( antenato del calcolo integrale), Teodoro di Cirene, Teeteto, Archita di Taranto.
Aristotele, nell’ambito della logica, Menecmo, Autolico di Pitane. Eudemo di Rodi nell’ambito della storia e dell’astronomia.
Nel 529 d.C. l’imperatore Giustiniano (482-565 d.C), rigido custode dell’ortodossia cristiana, chiuderà la scuola filosofica di Atene, lontana erede dell’Accademia platonica, considerata ormai come un intollerabile covo di paganesimo e di libertà di pensiero.
PERSONAGGI DEL V Secolo a.C.
ANASSIMENE di MILETO (586 – 528 a.C.) Di lui sappiamo solo quanto scrissero filosofi successivi, tra cui Aristotile. E’ considerato l’ultimo dei tre filosofi della Scuola di Mileto, considerati i primi filosofi del mondo occidentale, Anassimene è meglio conosciuto e identificato come un giovane amico o studente di 
Anassimandro, a sua volta allievo del primo filosofo Talete. Prima di lui Talete propose che tutto fosse fatto d’acqua; Anassimene che tutto fosse fatto di aria, o letteralmente di aer, che può anche includere nebbia o vapore. Aria più condensata compone oggetti più freddi e densi e quella più rarefatta oggetti più caldi e leggeri. Gran parte del suo pensiero astronomico tuttavia era basato su quello di Anassimandro, sebbene ne alterasse le idee per adattarle meglio alle sue opinioni filosofiche sulla fisica e sul mondo naturale. Anassimene riteneva che la Terra fosse piatta come un disco e si spostasse nell’aria come un frisbee. Il cratere di Anassimene sulla Luna è chiamato così in suo onore.
ARCHITA da TARANTO (428-360 a.C.). Fu filosofo e statista. Appartenente alla “seconda generazione” della scuola pitagorica, ne incarnò i massimi principi secondo l’insegnamento dei suoi maestri Filolao ed Eurito. Archita è considerato l’inventore della Meccanica razionale e il fondatore della Meccanica. Scopri’ la media armonica importante in statistica: dati n numeri considero n diviso la somma degli inversi dei numeri dati. (dati a, b,c ho 3 diviso 1/a+1/b+1/c). Lavorò sulla duplicazione del cubo.
DEMOCRITO di Abdera (460-362 a.C.). Presocratico, allievo di Leucippo (V sec. a.C.) e contemporaneo di Socrate (470-699) e dei suoi primi discepoli, quali Platone (428-348), muore probabilmente centenario. Si sa che visse tra agi e ric-chezze, prima di rinunciare a parte dei suoi beni per dedicarsi agli studi e ai viaggi. Sembra sia giunto in Egitto, in Etiopia e in India. E ovviamente ad Atene. E’ il filosofo dell’atomismo che identifica il pieno con la materia e il vuoto con lo spazio in cui la materia si muove. La materia è costituita, poi, da atomi, particelle ultime della materia, indivisibili. Gli atomisti, che in D. si indentificano giungomo al concetto di atomo per via teorica. Democrito e gli atomisti affermano che la divisibilità all’infinito , a furia di dividere la materia, dissolverebbe la materia nel nulla, giungendo alla non-materia.
EMPEDOCLE di Agrigento (490-430 a.C) presocratico. E’ uno dei tre fisici pluralisti (Empedocle d’Agrigento – 
Anassagora di Clazomene – Democrito di Abdera). è stato il primo a formulare una gnoseologia o teoria della conoscenza : La conoscenza si verifica quando avviene l’incontro fra una qualità presente nelle cose e una in noi identica a quella ( il simile conosce il simile). Secondo lui ogni individuo lascia tracce che i nostri sensi percepiscono. La filosofia di Empedocle si presenta come un tentativo di combinazione sintetica delle precedenti dottrine ioniche, pitagoriche, eraclitee e parmenidee. Da quest’ultime accoglie la tesi dell’immutabilità e dell’eternità dell’Essere, ovvero che nulla nasce e nulla muore. Dalle altre accetta l’idea del divenire, del continuo e incessante mutamento delle cose. Empedocle – e come lui anche gli altri fisici pluralisti – cerca di risolvere questa contraddizione distinguendo la realtà che ci circonda, mutevole, dagli elementi primi, immutabili, che la compongono.Negò con Anassagora l’unità qualitativa dell’essere, distingue tra la dimensione qualitativa e quella quantitativa delle cose, ammette una molteplicità per la seconda, mentre la esclude per la prima. Sostenne la teoria dei quattro elementi (terra-acqua-aria -fuoco), che chiama le radici di tutte le cose, che nascono dalle molteplici combinazioni delle stesse, combinazioni create da due forze: amore ed odio come forze attrattive e repulsive. Si occupò di ottica (L’ottica dei Greci).
ENOPIDE di CHIO (500-420 a.C.) noto per la scoperta dell’angolo esistente tra il piano dell’equatore celeste e lo zodiaco (il percorso apparente del Sole nel cielo in un anno), forse da attribuire a Pitagora, ma ad Enopide secondo Teone di Smirne (70-135). Sarà Eratostene (273-192 a.C) a misurare l’angolo con precisione. Enopide determinò anche un valore del “Grande anno”, il più piccolo intervallo di tempo che contiene un numero intero di anni e un numero intero di lunazioni. Enopide propose un grande anno composto di 59 anni solari. Articolo: S.Maracchia, la fama immeritata di Enopide di Chio.
EUDOSSO di CNIDO (408- 353 a.C.) fu studente di Platone (428/427-347 a.C.), ma anche di Archita di Taranto (428-360 a.C.), maestro di Menecmo (380-320 a.C.). Da Archita si presume sia stato avviato allo studio del problema della duplicazione del cubo, dei numeri interi e della teoria della musica. Si occupò del metodo di esaustione. A Cnido costruì un osservatorio astronomico e da lui vennero identificate varie costellazioni. Secondo Archimede sviluppò la teoria delle proporzioni che consentì di superare le difficoltà che si incontrano per trattare i numeri irrazionali; questa teoria sarà ripresa nel libro V degli Elementi di Euclide e in sostanza consente di trattare rigorosamente i numeri reali pensati come rapporti di grandezze. Si veda all’inizio di questa pagina web il modello delle: sfere concentriche dell’universo di Eudosso e Archimede.
Zu CHUNGZHI (Tsu Ch’ung-chih (429 – 500)) è un matematico cinese , astronomo e ingegnere vissuto durante la Dinastia Song. Scopre che il valore di π = 355/113 = 3,141592 9204 , è corretto fino alla sesta cifra, e in termini di frazioni è la migliore approssimazione frazionaria. La frazione è detta il numero di Zu Chongzhi. Fornisce una ulteriore limitazione per 3,1415926 < π < 3,1415927. A Zu Chongzhi dobbiamo la scoperta del volume di una sfera pari al nostre 4/3 πr3. il calcolo dell’anno fissato in 365,24281481 giorni, molto vicino agli attuali 365,24219878 giorni e molto vicino agli attuali 11,862. Si veda anche nel 1585 la riscoperta della frazione da parte di Adriaen Anthonisz (1541-1620). NOTA. Il valore π = 355/113 = (377-22)/(120–7) curiosamente si ottiene sottraendo membro a membro il valore tolemaico 377/120 dall’archimedeo 22/7.
IPPASO da METAPONTO (opera attorno al 500 a.C.) era certamente la persona più rilevante della scuola pitagorica, dopo Pitagora . Giamblico di Calcide (250 – 330), il biografo di Pitagora, gli attribuisce la descrizione del dodecaedro regolare e la dimostrazione della sua iscrivibilità in una sfera.Tuttavia, la sua relazione con i pitagorici fu alquanto burrascosa, in quanto divulgò pubblicamente un terribile segreto: la scoperta dell’incommensurabile. Per i Pitagorici i numeri erano solo i numeri naturali e le frazioni, ma la radice di 2 non poteva essere espresso in nessuna di queste forme, era un irrazionale e misurava un segmento incommensurabile con il lato.
IPPIA di ELIDE (443-343 a.C.) nel Peloponneso, fu filosofo e matema-tico. Con Protagora, Gorgia, Prodico, e, Trasimaco, egli forma il gruppo dei sofisti di prima generazione. Ideò una curva (quadratrice di I.), della quale si servì per risolvere il problema della trisezione dell´angolo e per questo la curva è anche nota come trisettrice, mediante la quale è possibile dividere un angolo in tre parti fra loro uguali. Successivamente, intorno alla metà del IV° secolo a.C. . Dinostrato, geometra, fratello di Menecmo, si servì della curva per risolvere il problema della quadratura del cerchio, da cui il nome di quadratrice, e mediante la quale è possibile rettificare la circonferenza ed escogitò anche uno strumento per costruire meccanicamente tale curva. Le critiche mosse da Platone nei confronti dell’uso di strumenti diversi dalla riga e dal compasso limitarono l’influenza dell’idea di Ippia nei successivi sviluppi della matematica greca.
IPPOCRATE di CHIO (460 -377 a.C.). Considerato il Padre della Medicina. Il Giuramento di Ippocrate (CLICCA)del IV Sec. (formula adattata il 13 giugno 2014) che viene prestato dai medici prima di iniziare la professione. Scrisse un libro “Elementi” a noi non pervenuto nel quale avrebbe anticipato Euclide di 100 anni. Un teorema di Ippocrate stabilisce che le aree di due cerchi stanno tra loro come i quadrati costruiti sui loro diametri. Il teorema è attribuito a Ippocrate di Chio, che lo utilizzò per la quadratura di particolari → lunule.Famosa la quadratura di una lunula che ha il suo nome!
PLATONE (427-347) Platone nacque ad Atene da genitori aristo-cratici: il padre Aristone, che vantava tra i suoi antenati Codro, l’ultimo leggendario re di Atene, gli impose il nome del nonno Aristocle; la madre, Perictione, secondo Diogene Laerzio discendeva dal famoso legislatore Solone. Fondamentale il suo incontro con Socrate che, dopo la parentesi del governo, oligarchico e filo-spartano, dei Trenta tiranni, del quale faceva parte il prozio di Platone, Crizia, fu accusato dal nuovo governo democratico di empietà e di corruzione dei giovani e condannato a morte nel 399 a.C. . Nell’Apologia di Socrate l’allievo descrive il processo del maestro, che pronuncia la sua difesa, denuncia la falsità di chi l’accusa di corrompere i giovani e come testimoni della sua condotta menziona un gruppo di suoi amici presenti nel tribunale, tra i quali «Adimànto, figlio di Aristòne, di cui Platone, qui presente, è fratello». Tuttavia nel Fedone, il narratore Fedone di Elide riferisce a Echecrate che Platone non era presente alle ultime ore di vita di Socrate.
Protagora (490 – 415/411 a.C.)
SOCRATE (470- 399 a.C ) non scrisse nulla, non lasciò testimonianza di sé, perché preferiva il contatto diretto e immediato con le persone, attraverso la parola; ma per fortuna abbiamo testimonianze indirette su di lui che sono giunte in particolare da Platone (428-348), suo discepolo. Finito il governo di Pericle, Atene su governata da 30 tiranni, e una volta caduti anche questi si restaurò lademocrazia. Socrate operò proprio nel periodo di restauro della democrazia, in cui quest’ultima era molto debole, incerta, precaria, e fu condannato a morte quindi in un periodo in cui il potere avvertiva una grave minaccia nelle critiche di un personaggio come lui. Fu accusato si non onorare le gli dei della sua città, di aver importato nuove divinità e di corrompere i giovani. Tali accuse erano quanto meno strane e celavano la forte preoccupazione del nuovo governo per un personaggio che mettendo in dubbio ogni certezza poteva minare la basi di un sistema già in bilico.
Zenone di Elea (489-431 a.C.) è stato un filosofo greco antico presocratico della Magna Grecia e un membro della Scuola eleatica fondata da Parmenide. Aristotele lo definisce inventore della dialettica. È conosciuto soprattutto per i suoi paradossi, che Bertrand Russell definì come smisuratamente sottili e profondi.
Articolo: Fontana -Toffalori su Zenone.
IV secolo a.C. (400-301)
EUCLIDE (330-247 a.C.) di Alessandria (scheda) .Matematico greco, che operò tra il 320 e il 270 a. C., ad Alessandria forse in coincidenza con la creazione della grande Biblioteca, avvenuta poco dopo il 300 a.C. proprio ad Alessandria. Euclide è ben noto per gli Elementi , un’opera contenente quel -li che erano i fondamenti del-la matematica in al tempo in una semi-empirica struttura assiomatica. Euclide fornisce un elenco di cinque postulati e di cinque nozioni comuni (o assiomi). Gli assiomi sono da intendere come qualcosa che veniva accettato come evidente, i postulati come qualcosa che doveva essere richiesto. Oggi i termini sono sinonimi.
Gli Elementi constano di 13 libri, ma in molte edizioni antiche compaiono altri due libri che la critica più recente attribuisce rispettivamente a Ipsicle (II secolo a.C.) e a Isidoro di Mileto (V-VI secolo d.C.).
NOTA. Gli Elementi, nei loro contenuti, erano stati sviluppati da vari autori, ma senza una reale sistematicità, presente invece negli Elementi. Così l’opera fu di influenza fondamentale per lo sviluppo del pensiero e della cultura occidentale. L’opera in ogni caso non si adegua all’esposizione elementare, ed è troppo difficile e astratta a causa del suo impianto logico. Il metodo deduttivo che appare in forma rigorosa e sistematica è parere di molti storici che risalga a Ippocrate di Chio (470- 410 a. C.), il quale un secolo prima di Euclide scrisse un’opera intitolata Elementi, della quale non è stato conservato neppure un frammento. Comunque è ad Ippocrate che si deve l’idea della dimostrazione per assurdo. Tuttavia sono gli Elementi i primi a presentare un assetto così rigorosamente assiomatico. Dei cinque assiomi (così come delle numerose definizioni) proposti da Euclide , uno (il quinto, che tratta nei fatti dell’unicità della parallela) venne considerato speciale fin dall’antichità. Questo testo è stato tramandato grazie alla prima ricostruzione che ne fece Teone di Alessandria, che fu tradotta in latino a Adelardo di Bath. Nel 1270, la traduzione di Adelardo fu riveduta, anche alla luce di altre fonti arabe (a loro volta derivate da altre versioni greche del manoscritto di Teone) da Campano da Novara. Questa versione (o una copia di una copia) venne stampata a Venezia nel 1482. Successivamente, sono state ritrovate altre versioni greche del manoscritto di Teone e una copia greca che probabilmente è precedente a quella di Teone. La ricostruzione attuale si basa sulla versione del filologo danese J. L. Heiberg risalente al 1880 e su quella dello storico inglese T. L. Heath del 1908. La prima traduzione in lingua cinese dal latino fu opera del gesuita Matteo Ricci, nel 1607. La prima edizione italiana è dovuta al matematico italiano Federigo Enriques e risale al 1935. Nel 1970 compare nei tipi della UTET un’altra versione italiana, tradotta da Lamberto Maccioni e commentata da Attilio Frajese. Riguardo ad ulteriori traduzioni in latino, le più antiche sono tutte attestate a cavallo tra il XV e il XVI secolo. Le traduzioni in lingua latina maggiormente accreditate, però, risalgono a XVII e XVIII secolo e, in ordine cronologico, le più avvalorate sono quelle del Barrow (1639), del Borelli (1658), del Keill (1701), del Gregory (1703), e del Simson, considerata una delle, se non la più prestigiosa, tanto da essere tutt’oggi il primo testo di riferimento per i geometri scozzesi (1756). A proposito, invece, della traduzione in italiano, la prima risale al 1543 ed è frutto dell’interpretazione e dell’elaborazione di Nicolò Tartaglia. Più recenti, invece, sono le traduzioni, dei soli libri geometrici, del Viviani, del Grandi e del Flauti (rispettivamente XVII, XVII e XIX secolo).
ARISTARCO di SAMO (310-230 a.C.), detto l’antico Copernico, per avere per primo introdotto una teoria astronomica nella quale il Sole e le stelle fisse sono immobili mentre la Terra ruota attorno al Sole e percorre una circonferenza. Sappiamo che Aristarco concordava con Eraclide Pontico nell’attribuire alla terra anche un moto di rotazione diurna attorno ad un asse inclinato rispetto al piano dell’orbita intorno al Sole, ipotesi che giustificava l’alternarsi delle stagioni. Allievo di Stratone di Lampsaco (335 –274 a.C.), città sullo stretto dei Dardanelli. Aristarco scrisse “Sulla grandezza e le distanze del sole e della luna dalla terra“. Giacomo Leopardi nella sua Storia dell’astronomia scrive: Altro astronomo greco fu Aristarco, vissuto, come credesi, verso il 264 avanti Gesù Cristo, benché considerevolmente più antico lo facciano il Fromondo e il Simmler presso il Vossio, ripresi però dal Fabricio. Di lui fecer menzione Vitruvio, Tolomeo e Varrone presso Gellio nel quale, in luogo di Aristide Samio, è da leggersi Aristarco. Egli determinò la distanza del Sole dalla Terra, che egli credé 19 volte maggiore di quella della Terra medesima dalla Luna e trovò la distanza della Terra dalla Luna, di 56 semidiametri del nostro globo. Credette che il diametro del sole fosse non più che 6 o 7 volte maggiore di quello della Terra e che quello della Luna fosse circa un terzo di quello della Terra medesima. Fu dogma di Aristarco il moto della Terra, ed egli, per tale opinione, reputossi da Cleante reo di empietà, quasi avesse turbato il riposo dei Lari e di Vesta. Sembra che Plutarco asserisca essere stato Cleante e non Aristarco il fautore del moto della Terra, così leggesi nel suo libro de facie in orbe Lunae.”Si occupò degli inizi della Trigonometria . cfr. Matematica/Compl Sc. Second./Sviluppo stor.della Trigonometria.
ARISTEO (340?-300? a.C.) allievo di Eudosso (408- 353 a.C.), fu forse una delle fonti principali cui attinse Euclide (330-247 a.C.)del quale era di poco più vecchio. Scrisse un trattato sulle coniche ed uno sui poliedri regolari.
ARISTOTILE di STAGIRA (384- 322 a.C.)
Fu il padre della Logica. e del sillogismo, è considerato uno dei maggiori filosofi dell’Occidente.
AUTOLICO di PITANE (360-290 a:C.). Si conoscono le opere: a prima è Sul moto della sfera (De sphaera quae movetur liber.) sulla geometria della sfera, di interesse per l’astronomia. Ancora Sulle levate e tramonti degli astri (De vario ortu et occasu astrorum inerrantium) in due libri, il secondo è un’edizione rivista e ampliata del primo.
DINOSTRATO di APECONNESSO (390 a.C. – 320 a.C.) in Tracia, oggi in Turchia. Fu un matematico, fratello di Menecmo (380-320 a.C.) . D. è noto per aver usato la quadratrice (una curva trascendente scoperta da Ippia (443- 343 a.C.) di Elide) per risolvere il problema della quadratura del cerchio. Dei suoi lavori ci è giunto ben poco.
EPICURO di Samo (341-270) a 18 anni si recò ad Atene, qui a 32 anni iniziò ad insegnare e nel 306 a.C. Discepolo dello scettico democriteo Nausifane e fondatore di una delle maggiori scuole filosofiche dell’età ellenistica, che, come altre scuole filosofiche greche, assunse un carattere religioso. La filosofia di Epicuro, l’epicureismo, si compone di teoria della conoscenza, etica e fisica ed ha come fine il raggiungimento della felicità, che si identifica con la liberazione dalla passioni, dai desideri e dalle opinioni incerte e mutevoli. L’epicureismo, quindi, abbandona la ricerca speculativa fine a se stessa e si rivolge all’interiorità dell’uomo, cioè è una filosofia sostanzialmente individualistica. In Fisica Epicuro prende da Democrito il principio del materialismo e del meccanicismo universali e cerca nella materia la spiegazione della natura. Egli sostiene che ogni cosa è corpo e il nascere e morire delle cose è un processo di aggregazione e disgregazione dei corpi più semplici che egli chiama atomi, qualitativamente omogenei, infiniti, invisibili, ingenerati ed indistruttibili. 
Fondata su queste basi la dottrina di Epicuro, afferma che la sensazione è sempre vera; essa è, pertanto, materialistica ed esclude ogni intervento di tipo divino sul mondo. Epicuro fu scrittore prolifico, ma di lui restano solo, attraverso Diogene Laertio, tre lettere e le Massime capitali; molti frammenti della sua opera principale, Sulla natura, e delle sue lettere sono stati scoperti nei papiri di una villa di Ercolano nel 1752/54.
Le opere non pervenute sono state tramandate da manoscritti arabi. Le creazioni di Erone (clicca).
MENECMO di APECONNESSO (380-320 a.C.) in Tracia, oggi in Turchia. Fu fratello di Dinostrato (390 a.C. – 320 a.C.) ed allievo di Eudosso di Cnido (408- 353 a.C.). E’ famoso per aver essere stato il primo a studiare le sezioni coniche, che furono dette “triadi di Menecmo” e per aver data una soluzione (ovviamente approssimata) al problema della duplicazione del cubo, usando parabola ed iperbole. Fu i forse da Apollonio (262 – 190 a.C), successivamente primo a mostrare che ellissi, parabole ed iperboli sono sezioni di un cono con un piano non parallelo alla base. Si ritiene che NON sia stato Menecmo ad inventare i nomi di parabola ed iperbole; dati.
Eraclito PONTICO (385-310 a.C.) filosofo (vedi Aristarco).
STRATONE di Lampsaco (335 –274 a.C.), (città sullo stretto dei Dardanelli) fu maestro di Aristarco.
III secolo a.C. (300- 201)
APOLLONIO da PERGA (262-190 a.C), è stato un matematico famoso per le sue opere sulle sezioni coniche e l’introduzione, in astronomia, degli epicicli e deferenti. Fu attivo tra la fine del III e l’inizio del II secolo a.C., ma le scarse testimonianze sulla sua vita rendono impossibile una migliore datazione Fu lui che diede alla ellisse, alla parabola e alla iperbole i nomi con i quali da allora queste curve sono identificate.
ARCHIMEDE di Siracusa (287 – 212 a.C.) Fu uno dei più grandi scienziati della storia, i suoi contributi spaziano dalla geometria all’idrostatica, dall’ottica alla meccanica: fu in grado di calcolare la superficie e il volume della sfera e intuì le leggi che regolano il galleggiamento dei corpi. In campo ingegneristico, scoprì e sfruttò i principi di funzionamento delle leve e il suo nome è associato a numerose macchine e dispositivi, come la vite di Archimede, a dimostrazione della sua capacità inventiva. Circondate da mistero sono le macchine da guerra create da Archimede per difendere Siracusa dall’assedio romano. Fu ucciso da un soldato romano. Archimede dispose che sulla sua tomba fosse raffigurata una sfera e il cilindro circoscritto. Della tomba si era persa ogni traccia, ma Cicerone narra nelle Tusculanae disputationes che, al tempo che fu questore in Sicilia (75 a.C.), ritrovò la tomba sommersa dai rovi.
Si veda all’inizio di questa pagina web il modello delle: sfere concentriche dell’universo di Eudosso e Archimede. (vai a) Arte e Scienza in Archimede di L. Nicotra (Parte I )–( Partee II). Cfr. Andre Koch Torres Assis – Ceno Pietro Magnaghi, il-metodo-illustrato-di-Archimede-in-italiano.
Archimede di Siracusa dimostra che un cerchio equivale a un triangolo con base di lunghezza eguale a quella della circonferenza e altezza di lunghezza guale a quella del raggio. Fu il primo ad approssimare scienti-ficamente pi-greco utilizzando poligoni regolari inscritti e circoscritti a una circon-ferenza. Aumentando il numero di lati il rapporto tra il perimetro e l’area limita supe-riormente e inferiormente� . Utilizzando poligoni di 96 lati lo scienziato siracusano scoprì che: 3,140845 …= 3+10/71= 223/71 < π < 22/7 = 3+10/70 = 2,1428571….
ERATOSTENE di CIRENE (273-192 a.C) Studiò i numeri primi ed inventò il famoso dai rovi. Crivello di E. Fu il primo ad aver misurato il diametro terrestre e la CIR-CONFERENZA TERRESTRE, in ragione di 40.500 km circa (un valore sorprendentemente vicino al vero di 39.941 km). Misurò la distanza del sole dalla luna e l’inclinazione dell’asse terrestre. Da ricordare che la sfericità della Terra era già tra le convinzioni dei matematici greci, come pure
la grande distanza che la separa dagli altri corpi celesti. La misura di Eratostene. Si occupò anche della duplicazione del cubo. Vedasi anche POISEIDONIO (135-51 a.C.).
CTESIBIO di ALESSANDRIA (285-222 a.C.) è stato un ingegnere e inventore greco antico, inventore della pompa, dell’organo a canne e dell’orologio ad acqua, fondatore della pneumatica e iniziatore della scuola dei meccanici alessandrini.
scheda su Ctesibio (per saperne di più).
FILONE di Bisanzio (280-220 a.C). E’ stato uno scienziato e fisico greco vissuto nel III secolo a.C., presumibilmente tra il 280 e il 220; i soli dati biografici conosciuti sono la sua nascita a
Bisanzio, il suo trasferimento ad Alessandria e la sua permanenza per qualche tempo a Rodi; si è occupato di meccanica e di ingegneria civile e militare e perciò fu detto Philo Mechanicus. Successore e discepolo di Ctesibio, che cita ripetutamente nei suoi scritti, di lui egli perfezionò alcune scoperte in campo pneumatico e in ambito balistico, anche se la loro conoscenza personale è dubbia. Per saperne di più.
E
Ugo di San Vittore (n. 1141) che definì la matematica e la fisica come scienze astratte, infatti la matematica astrae dalla realtà gli elementi che sono confusi insieme come per esempio la linea che non esiste da sola, ma è accompagnata da un certo spessore, mentre la fisica astrae gli elementi che nei corpi sono confusi e cioè aria, acqua, terra e fuoco, i quali a loro volta sono formati da atomi. Egli affermò anche che la materia non si può distruggere né creare.
DIOCLE di Caristo (240–180 a.C.). Ci sono giunti brani di un trattato Sugli specchi ustori. In uno di questi frammenti è trattata la soluzione del problema della duplicazione del cubo che, all’epoca, insieme alla quadratura del cerchio e alla trisezione dell’angolo, formavano i cosiddetti problemi di Delo, veri rompicapo per le conoscenze di geometria e matematica del tempo. Nota la famosa cissoide di Diocle. La sua soluzione, originale, procede per individuazione di due medi proporzionali, ricorrendo ad una curva, oggi nota come cissoide di Diocle. Questo problema è collegato a quello analogo, trattato già nel V secolo a.C. da Ippocrate di Chio, per riduzione del problema stesso a quello di trovare due medi proporzionali a due segmenti dati, il maggiore dei quali è doppio del minore. La soluzione di Diocle è riferita da Eutocio insieme ad altre 8 soluzioni di altrettanti matematici greci. Inoltre, tramite Eutocio, possediamo la soluzione di Diocle al problema archimedeo della sezione di una sfera con volumi delle calotte vincolati a stare tra loro in un rapporto assegnato, algebricamente equivalente alla soluzione di un’equazione cubica. La soluzione di Diocle prevede l’intersezione di un’ellisse con un’iperbole. 
Quanto all’opera menzionata Sugli specchi ustori, si sa che era di ampio respiro: discuteva di specchi concavi a profilo sferico ed ellissoidale, (per l’ellissoide ottenuto dalla rotazione dell’ellisse intorno al suo asse maggiore). Il caso paraboidale è considerato nella parte del trattato pervenutaci in arabo e la trattazione si basa sulla proprietà focale della parabola. L’opera di Diocle fu apparentemente poco conosciuta dai matematici greci successivi, ma influenzò i matematici arabi e in particolare al-Haytham. Fu Guglielmo di Moerbeke (1215–1286), a curare la prima traduzione in latino dei frammenti superstiti di Diocle. Gerald James Toomer (1934) Toomer, nel 1976, pubblicò il testo arabo. In un’opera sugli specchi ustori risolse per mezzo di due coniche il problema di dividere con un piano una sfera in due parti di rapporto prestabilito; il problema, già formulato da Aristotele, era stato risolto solo parzialmente da Archimede. Definì inoltre una curva, detta cissoide, di cui si servì per risolvere il problema della duplicazione del cubo.
FILONE di BISANZIO (280 – 220 a.C.). Fisico, allievo di CTESIBIO, autore di un trattato di meccanica in 9 libri in cui si trattava di tecnica guerresca, della costruzione dei porti e di macchine pneumatiche. F. è ricordato da Vitruvio ed Erone. Della sua opera sono rimasti il 4º libro ed estratti o traduzioni di altri.
Liu HUI (220? – 280 ?) matematico cinese, vissuto nel Regno Wei. Nel 263 scrisse e pubblicò un libro con soluzioni a problemi. Lavora dapprima su un poligono di 96 lati, poi trova π = 3,14159 da un poligono di 3072 lati, scrive anche . π = 157/50 = 314/100 = 3,14. Si noti che 157 è primo ed è la metà di 314.
II secolo a.C. (200-101)
Ipparco di Nicea, il “padre della trigonometria” e Teodosio di Bitinia, astronomo.
IPPARCO di NICEA (200-120 (II sec.) a.C.). Noto per la scoperta della precessione degli equinozi. Sviluppò accurati modelli per spiegare il moto del Sole e della Luna, servendosi delle osservazioni e delle conoscenze accumulate nei secoli dai Caldei Babilonesi, e fu il primo a stimare con precisione la distanza tra la Terra e la Luna. Grazie alle sue teorie sui moti del Sole e della Luna e alle sue nozioni di trigonometria, della quale è ritenuto il fondatore, è stato probabilmente il primo a sviluppare un affidabile metodo per la previsione delle eclissi solari e lunari. Il suo operato include la scoperta della precessione degli equinozi, la compilazione di un celebre catalogo stellare e, probabilmente, l’invenzione di un tipo di astrolabio. Grazie all’osservazione di una stella che vide apparire, probabilmente una nova nella costellazione dello Scorpione,avanzò l’ipotesi, ardita per l’epoca, che le stelle non fossero fisse, ma in movimento. È inoltre stato il primo a compilare una tavola trigonometrica, che gli permetteva di risolvere qualsiasi triangolo. Per la Trigonometria,cfr. in questo sito : Matematica/Complementi Scuola Secondaria/Sviluppo storia della Trigonometria.
IPSICLE (190-120 a.C.) è stato un matematico e astronomo greco antico noto per le sue opere dai titoli Ascensioni Si pensa che sia in quest’opera che è stata adottata la divisione del cerchio in 360 gradi, poiché divide il giorno in 360 parti, soluzione forse suggerita dall’astronomia babilonese. E’ maggiormente noto per essere il possibile utore dell’apocrifo Libro XIV degli “Elementi” di Euclide”, che potrebbe essere stato scritto sulla base di un trattato di Apollonio di Perga. Il libro continua l’analisi di Euclide dei solidi regolari inscritti in sfere, giungendo al risultato secondo cui il rapporto delle superfici del dodecaedro e dell’icosaedro inscritti nella stessa sfera è il medesimo del rapporto dei loro volume, essendo tale rapporto . (Cfr. Euclide e Isidoro di Mileto (442-537) ).
. (Cfr. Euclide e Isidoro di Mileto (442-537) ).
POSIDONIO di Apamea, detto di Rodi (135-51a.C.). Fu uno stoico, considerato il più grande filosofo della sua epoca, tanto che, per l’ampiezza degli studi, fu soprannominato “Atleta”. Usò lo stesso metodo di Eratostene (273-192 a.C), per la misura della circonferenza terrestre, ma partì dalla distanza fra Rodi e Alessandria, usando la differenza di altezza della stella Canopo sul meridiano dei due luoghi, calcolò una circonferenza terrestre di 240.000 stadi (38.000 km circa), valore vicino a quello trovato da Eratostene, ma a quanto pare frutto di due errori che si compensavano.esplicativi forniti dalla mitologia, anche se ancora lontano dal metodo sperimentale.
TEODOSIO di Bitinia (160-100 a.C.), noto anche come Teodosio Tripolita, è stato un matematico e astronomo greco antico.
I secolo a.C. (100-001)
Marco Vitruvio POLLIONE(80-15 a.C.) calcola π come frazione e assegna π=25/8 = 3,125 .
New mail
l